引言
现代金融领域的计量工作分为两大块，即资产定价和风险度量。而资产定价又是以度量风险并为风险定价为基础，由此可见，风险度量工作实际上是现代金融计量领域的核心。金融领域度量风险的方法有很多，其中应用最多的是方差、最大回撤和VaR等。
目前，在业界，VaR不仅单纯作为风险管理的工具，在进行投资组合优化时，也会将VaR作为重要的过滤指标之一。
VaR的定义
VaR是Value at Risk的简称，中文译作“在险价值”。它是指在市场正常波动情况下，投资者所持有的投资组合在未来一定时期（$T$）内，在一定置信水平（$\alpha$）下所可能产生的最大可能损失。
假设投资者持有的投资组合的初始价值为$P_{0}$，$r$为未来一定时期（$T$）对应的收益率。那么，该组合的期末价值为：
$$P_{T}=P_{0}(1+r_{T})$$
\(r\)可视作随机变量，若假设在某一置信水平下，该投资组合的最低价值为$P^*$，则：
$$P_{T}^*=P_{0}(1+r_{T}^*)$$
显然，根据VaR的定义可知，其等于投资组合的最低价值和初始价值之差：
$$VaR_{\alpha}=-P_{0}r_{\alpha}^*$$
可见，计算VaR值等价于计算一定置信水平下的投资组合的最低价值$P^$或最低收益率$r^$。而计算最低价值或最低收益率则需依赖于价格序列或收益率序列的分布或概率密度函数。换句话说，计算金融资产序列的分布函数或概率密度函数正是计算VaR值的核心之处。
VaR的算法
清楚了VaR的定义，计算VaR的方法也就知道的差不多了。目前，常用的VaR算法可以分为参数法即方差-协方差法、蒙特卡洛模拟法以及非参数方法即历史模拟法。在VaR的应用过程中，人们也对VaR的上述算法进行了扩展。比如，在方差-协方差方法下人们提出了指数级权平均模型计算方差或者结合Garch类模型计算方差进而计算VaR的方法。
历史模拟法
历史模拟法是最简单的计算VaR的方法。它假设投资组合未来的波动与投资组合的历史数据完全一致，因此，计算投资组合的未来VaR就等同于计算历史数据的既有VaR。
历史模拟法的步骤为：
- 搜集历史数据
- 计算历史数据的几何收益率
- 对收益率进行排序并计算给定置信水平的下分位数
单资产VaR的计算及其R实现
下面以计算单个资产的VaR为例：
# 加载必要包
if (!require("quantmod")) install.packages("quantmod")
## 载入需要的程序包：quantmod
## 载入需要的程序包：xts
## 载入需要的程序包：zoo
##
## 载入程序包：'zoo'
## The following objects are masked from 'package:base':
##
## as.Date, as.Date.numeric
## 载入需要的程序包：TTR
## Registered S3 method overwritten by 'quantmod':
## method from
## as.zoo.data.frame zoo
library(quantmod)
# 获取苹果公司股票数据
getSymbols("AAPL", src = "yahoo", from = Sys.Date() - 365, to = Sys.Date())
## [1] "AAPL"
# 计算对数收益率
returns <- na.omit(periodReturn(AAPL, period = 'daily', type = 'log'))
# 设置置信水平 (95%)
confidence_level <- 0.95
# 历史模拟法计算VaR
historical_var <- -quantile(returns, probs = 1 - confidence_level)
# 打印结果
cat("历史模拟法计算的每日VaR（95%置信水平）:", round(historical_var*100, 2), "%\n")
## 历史模拟法计算的每日VaR（95%置信水平）: 3.12 %
# 可视化结果
hist(returns, breaks = 50, main = "日收益率分布与VaR（95%）",
xlab = "日收益率", col = "lightblue", border = "white")
abline(v = -historical_var, col = "red", lwd = 2)
text(x = -historical_var, y = par("usr")[4]*0.9,
labels = paste("VaR =", round(historical_var*100, 2), "%"),
pos = 2, col = "red")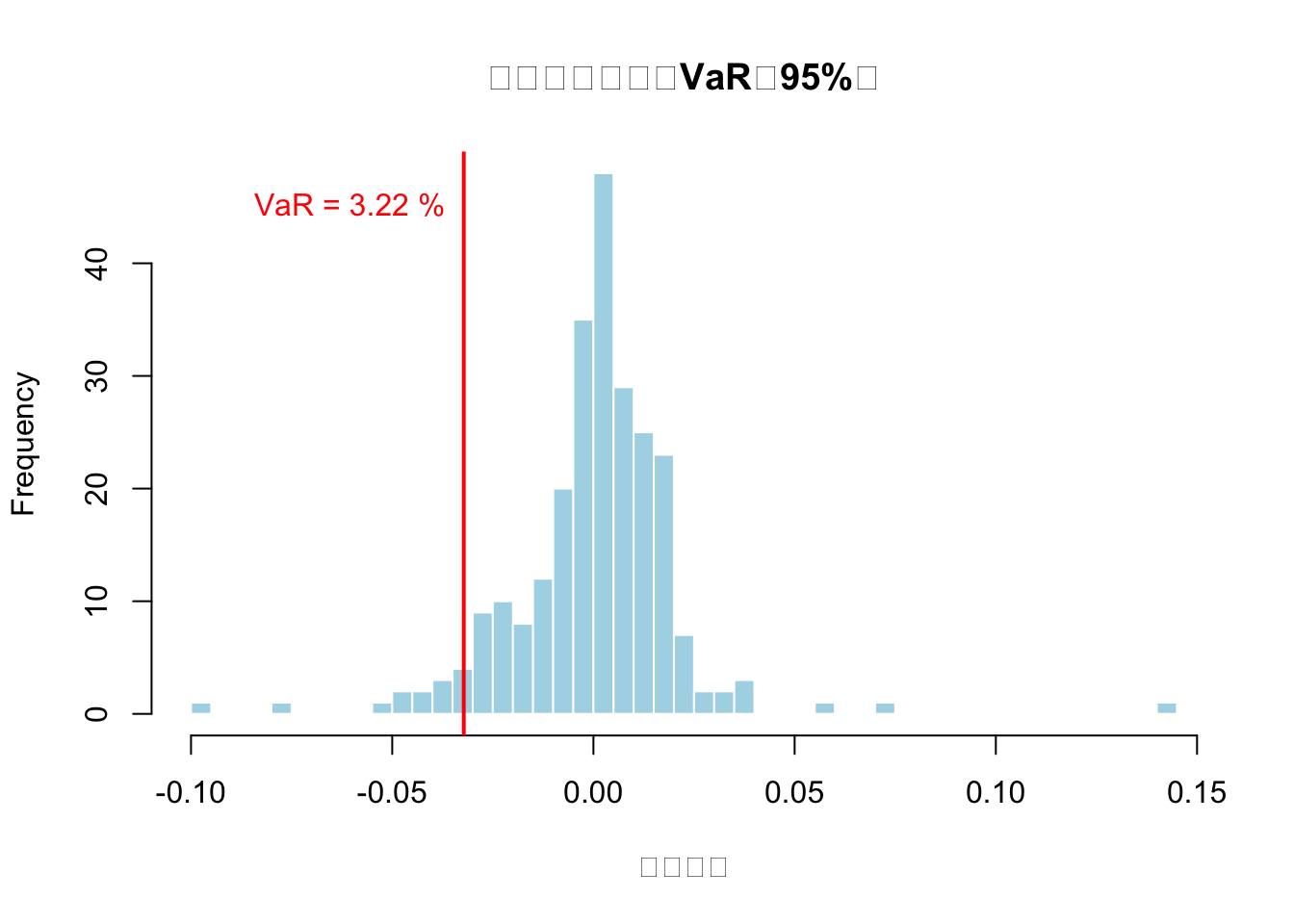
也可以直接用PerformanceAnalytics包中的VaR函数计算历史模拟法下的VaR值：
# 加载必要包
if (!require("quantmod")) install.packages("quantmod")
if (!require("PerformanceAnalytics")) install.packages("PerformanceAnalytics")
## 载入需要的程序包：PerformanceAnalytics
##
## 载入程序包：'PerformanceAnalytics'
## The following object is masked from 'package:graphics':
##
## legend
library(quantmod)
library(PerformanceAnalytics)
# 获取苹果公司股票数据（过去250个交易日）
getSymbols("AAPL", src = "yahoo", from = Sys.Date() - 365, to = Sys.Date())
## [1] "AAPL"
# 计算对数收益率
returns <- na.omit(ROC(Cl(AAPL))) # 等效于 log(Cl(AAPL)/lag(Cl(AAPL)))
# 使用PerformanceAnalytics包计算历史模拟法VaR（95%置信水平）
var_result <- VaR(
R = returns,
p = 0.95,
method = "historical",
portfolio_method = "single"
)
# 提取并格式化结果
historical_var <- abs(var_result[1,]) # VaR值通常取正数表示损失
confidence_level <- attr(var_result, "cl")
# 输出结果
cat("PerformanceAnalytics计算的每日VaR（", confidence_level*100, "%置信水平）:",
round(historical_var*100, 2), "%\n")
## PerformanceAnalytics计算的每日VaR（ %置信水平）: 3.13 %
# 可视化收益率分布及VaR
hist(returns, breaks = 50, main = "日收益率分布与VaR（历史模拟法）",
xlab = "日收益率", col = "lightblue", border = "white")
abline(v = -historical_var, col = "red", lwd = 2)
text(x = -historical_var, y = par("usr")[4]*0.9,
labels = paste("VaR =", round(historical_var*100, 2), "%"),
pos = 2, col = "red")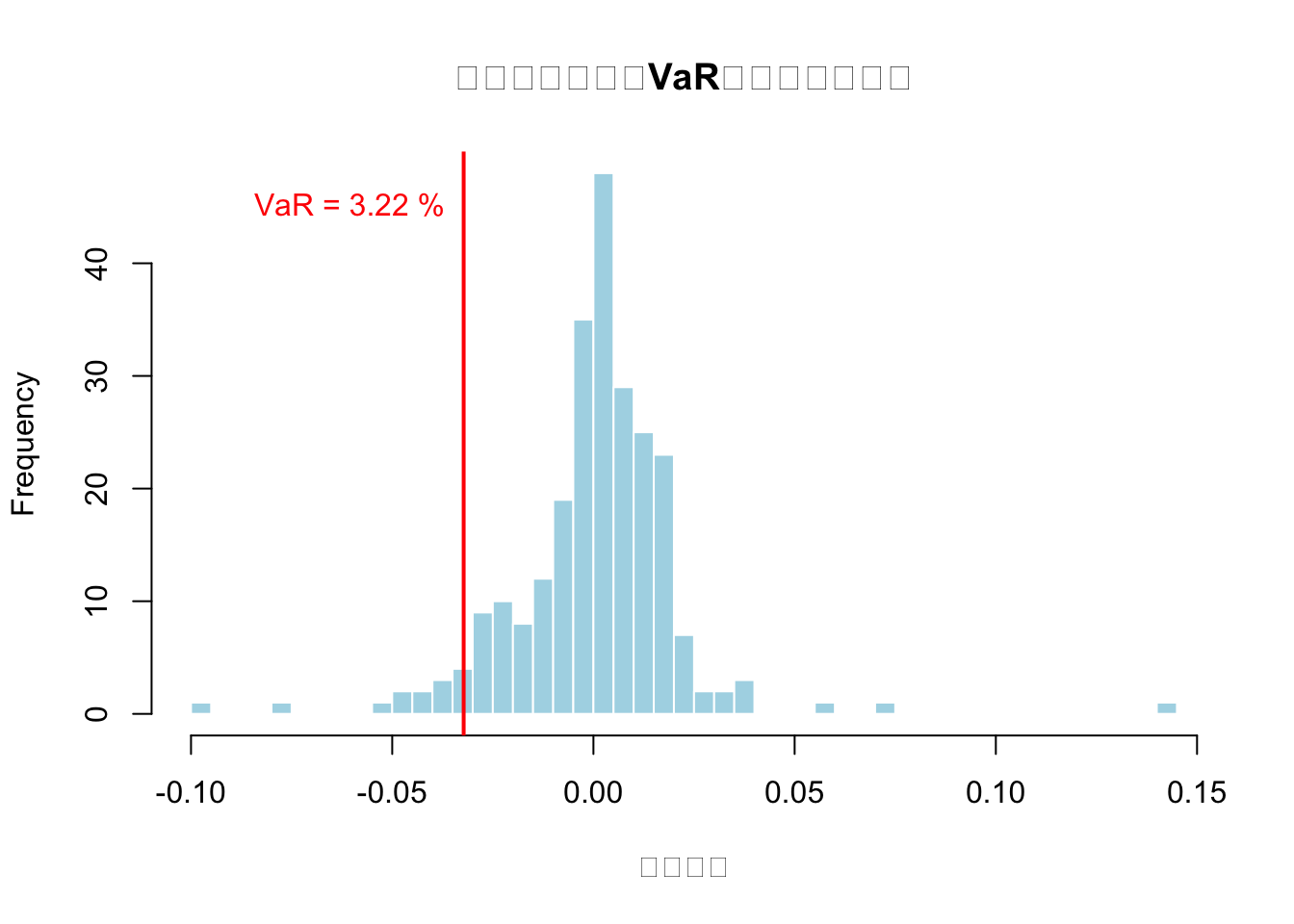
多资产投资组合的VaR计算及其R实现
用历史模拟法计算多资产投资组合的VaR与单资产思路类似，唯一不同的是要按照当前投资组合中各资产的权重计算投资组合的历史收益率。
具体R代码如下:
# 加载必要包
library(quantmod) # 金融数据获取
library(dplyr) # 数据处理
##
## ######################### Warning from 'xts' package ##########################
## # #
## # The dplyr lag() function breaks how base R's lag() function is supposed to #
## # work, which breaks lag(my_xts). Calls to lag(my_xts) that you type or #
## # source() into this session won't work correctly. #
## # #
## # Use stats::lag() to make sure you're not using dplyr::lag(), or you can add #
## # conflictRules('dplyr', exclude = 'lag') to your .Rprofile to stop #
## # dplyr from breaking base R's lag() function. #
## # #
## # Code in packages is not affected. It's protected by R's namespace mechanism #
## # Set `options(xts.warn_dplyr_breaks_lag = FALSE)` to suppress this warning. #
## # #
## ###############################################################################
##
## 载入程序包：'dplyr'
## The following objects are masked from 'package:xts':
##
## first, last
## The following objects are masked from 'package:stats':
##
## filter, lag
## The following objects are masked from 'package:base':
##
## intersect, setdiff, setequal, union
library(ggplot2) # 可视化
# ========== 参数设置 ==========
symbols <- c("AAPL", "GOOG", "MSFT") # 资产代码（苹果、谷歌、微软）
weights <- c(0.5, 0.3, 0.2) # 资产权重（总和为1）
portfolio_value <- 1e7 # 投资组合当前价值（假设1千万元）
confidence_level <- 0.95 # 置信水平
start_date <- "2020-01-01" # 数据开始日期
end_date <- "2023-12-31" # 数据结束日期
# ========== 1. 获取历史价格数据 ==========
getSymbols(symbols, src = "yahoo", from = start_date, to = end_date)
## [1] "AAPL" "GOOG" "MSFT"
# 提取收盘价并合并
prices <- merge(Cl(get(symbols[1])), Cl(get(symbols[2])), Cl(get(symbols[3])))
colnames(prices) <- symbols
# 清理缺失值（确保日期对齐）
prices_clean <- na.omit(prices)
# ========== 2. 计算各资产对数收益率 ==========
returns <- data.frame(
AAPL = as.numeric(Delt(prices_clean$AAPL)),
GOOG = as.numeric(Delt(prices_clean$GOOG)),
MSFT = as.numeric(Delt(prices_clean$MSFT))
) %>% na.omit() # 去除首行NA
# ========== 3. 计算投资组合每日收益率 ==========
# 将收益率转换为矩阵进行加权计算
returns_matrix <- as.matrix(returns)
portfolio_returns <- returns_matrix %*% weights
# ========== 4. 历史模拟法计算VaR ==========
# 按升序排列组合收益率（损失为负值）
sorted_returns <- sort(portfolio_returns)
# 确定分位数位置
n <- length(sorted_returns)
var_index <- floor((1 - confidence_level) * n)
var_quantile <- sorted_returns[var_index]
# 计算VaR绝对值
VaR <- abs(var_quantile) * portfolio_value
# ========== 5. 输出结果 ==========
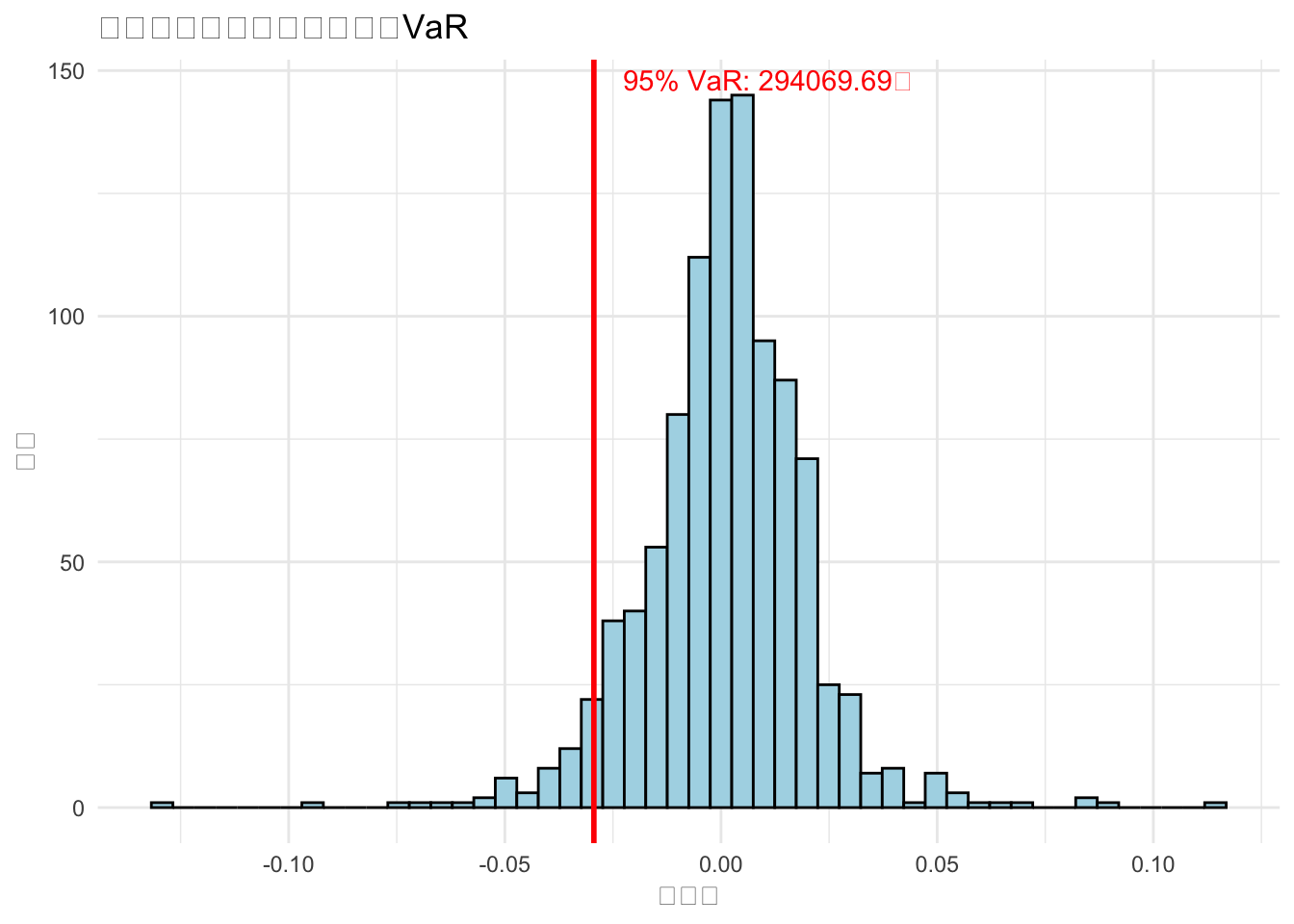
cat("========== 计算结果 ==========\n")
## ========== 计算结果 ==========
cat("置信水平:", confidence_level * 100, "%\n")
## 置信水平: 95 %
cat("历史数据天数:", n, "\n")
## 历史数据天数: 1005
cat("VaR分位数对应收益率:", round(var_quantile * 100, 2), "%\n")
## VaR分位数对应收益率: -2.94 %
cat("组合VaR值:", round(VaR, 2), "元\n")
## 组合VaR值: 294069.7 元
# ========== 6. 可视化== ==========
# 绘制组合收益率分布直方图
ggplot(data.frame(Return = portfolio_returns), aes(x = Return)) +
geom_histogram(bins = 50, fill = "lightblue", color = "black") +
geom_vline(xintercept = var_quantile, color = "red", linewidth = 1) +
labs(title = "投资组合历史收益率分布与VaR",
x = "收益率", y = "频数") +
annotate("text", x = var_quantile, y = Inf,
label = paste0(confidence_level * 100, "% VaR: ", round(VaR, 2), "元"),
color = "red", vjust = 1.5, hjust = -0.1) +
theme_minimal()
