指数加权移动平均法
指数移动加权法是一种动态波动率建模方法,其核心思想是通过赋予历史收益率随时间衰减的权重,捕捉金融时间序列的波动率聚集特征。与传统等权重方法不同,EWMA通过引入衰减因子 \(\lambda\),其中: \(\left(0\le\lambda\le1\right)\) ,使近期数据对波动率估计的影响呈指数级递增,而远期数据影响逐渐衰减(通常取 \(\lambda = 0.94\) ,基于RiskMetrics建议)。这种机制使得模型能更快响应市场突变,尤其适用于高频风险监测。
单资产情形
1. 数据准备与收益率计算
- 获取资产历史收盘价序列${P_t}$,计算对数收益率: $$ r_t = \ln\left(\frac{P_t}{P_{t-1}}\right) $$
2. 动态方差估计
EWMA通过指数衰减因子 \(\lambda\) 赋予近期数据更高权重,捕捉波动率的时变特性:
$$ \sigma_t^2 = \lambda \sigma_{t-1}^2 + (1-\lambda) r_{t-1}^2 $$
其中:
\(\lambda \in (0,1)\):衰减因子(典型值0.94)\(r_{t-1}\):前一日收益率\(\sigma_{t-1}^2\):前一日波动率
3. VaR计算(正态假设)
- 单日VaR公式: $$ \text{VaR}_{\alpha} = -\mu + \sigma_t \Phi^{-1}(1-\alpha) $$ 其中$\mu$为收益率均值(短期内可忽略),$\Phi^{-1}$为标准正态分布分位数(如95%置信水平对应1.645)
4. 多期VaR调整
- 持有期$T$天的VaR扩展: $$ \text{VaR}T = \text{VaR}{1d} \times \sqrt{T} $$
代码实现
# 加载必要包
if (!require("quantmod")) install.packages("quantmod") # 金融数据获取
## 载入需要的程序包:quantmod
## 载入需要的程序包:xts
## 载入需要的程序包:zoo
##
## 载入程序包:'zoo'
## The following objects are masked from 'package:base':
##
## as.Date, as.Date.numeric
## 载入需要的程序包:TTR
## Registered S3 method overwritten by 'quantmod':
## method from
## as.zoo.data.frame zoo
if (!require("ggplot2")) install.packages("ggplot2") # 可视化
## 载入需要的程序包:ggplot2
library(quantmod)
library(ggplot2)
# 获取标普500指数数据(示例)
getSymbols("^GSPC", src = "yahoo", from = "2020-01-01", to = Sys.Date())
## [1] "GSPC"
# 计算对数收益率
returns <- na.omit(ROC(Cl(GSPC))) # 使用收盘价计算
colnames(returns) <- "Daily_Return"
# 参数设置
lambda <- 0.94 # 衰减因子
portfolio_value <- 1e6 # 组合价值100万美元
confidence_level <- 0.95 # 置信水平
z_score <- qnorm(1 - confidence_level) # 分位数(正态分布)
# 初始化EWMA方差序列
n <- length(returns)
ewma_var <- numeric(n)
ewma_var[1] <- var(returns) # 初始化为样本方差
# 递归计算EWMA方差
for (i in 2:n) {
ewma_var[i] <- lambda * ewma_var[i-1] + (1 - lambda) * returns[i-1]^2
}
# 转换为年化波动率
ewma_vol <- sqrt(ewma_var * 252)
# 计算VaR序列
VaR <- portfolio_value * z_score * ewma_vol
# 获取最新VaR值
latest_VaR <- tail(VaR, 1)
cat("最新EWMA VaR(95%置信度):", round(latest_VaR, 2), "美元\n")
## 最新EWMA VaR(95%置信度): -581585.7 美元
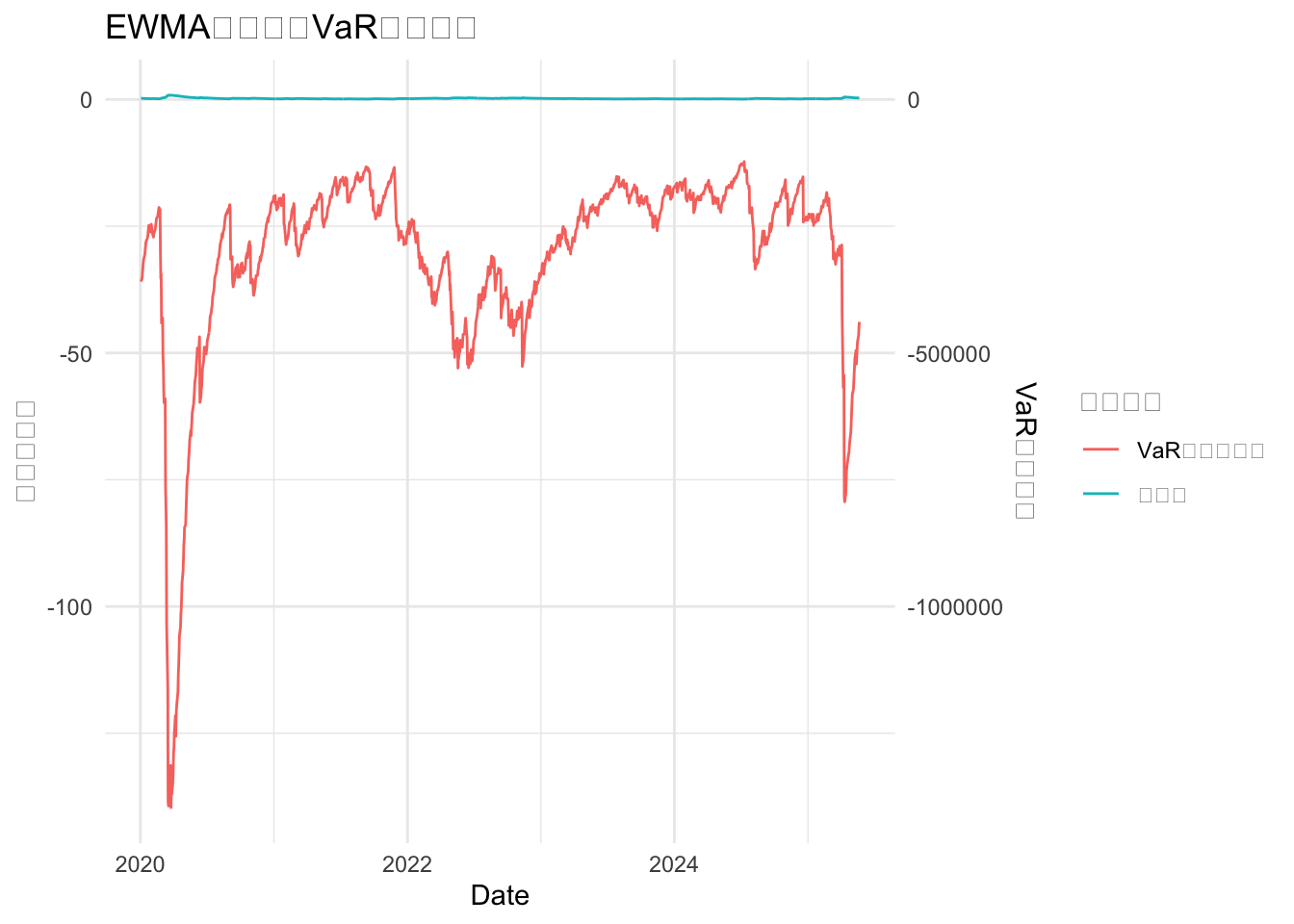
# 可视化结果
results <- data.frame(
Date = index(GSPC)[-1],
Volatility = ewma_vol,
VaR = VaR
)
ggplot(results, aes(x = Date)) +
geom_line(aes(y = Volatility, color = "波动率")) +
geom_line(aes(y = VaR / 1e4, color = "VaR(万美元)")) +
scale_y_continuous(
name = "年化波动率",
sec.axis = sec_axis(~ . * 1e4, name = "VaR(美元)")
) +
labs(title = "EWMA波动率与VaR动态变化",
color = "指标类型") +
theme_minimal()
多元资产组合EWMA-VaR建模原理与R实现
协方差矩阵动态更新
多资产EWMA模型通过递归更新协方差矩阵捕捉资产间相关性的时变特征:
$$ \Sigma_t = \lambda \Sigma_{t-1} + (1-\lambda)\mathbf{r}{t-1}\mathbf{r}{t-1}^\top $$
其中:
\(\mathbf{r}_{t-1}\):前一期资产收益率向量($n \times 1$)\(\Sigma_{t-1}\):前一期协方差矩阵($n \times n$)\(\lambda\):衰减因子(建议值0.94):ml-citation{ref=“4,8” data=“citationList”}
组合VaR计算流程
| 步骤 | 计算公式 |
|---|---|
| 组合方差 | \(\sigma_p^2 = \mathbf{w}^\top \Sigma_t \mathbf{w}\) |
| 年化波动率 | \(\sigma_p^{\text{annual}} = \sigma_p \sqrt{252}\) |
| VaR | \(VaR_{\alpha} = Z_{1-\alpha} \times P_0 \times \sigma_p^{\text{annual}}\) |
\(\mathbf{w}\):资产权重向量(需满足$\sum w_i=1$)\(P_0\):组合总价值
R语言完整实现
# 加载必要库
library(quantmod) # 多元金融数据获取
library(ggplot2) # 可视化
library(reshape2) # 数据重塑
# 获取三大股指数据
symbols <- c("^GSPC", "^IXIC", "^DJI") # 标普500、纳斯达克、道琼斯
getSymbols(symbols, from = "2020-01-01", to = Sys.Date())
## [1] "GSPC" "IXIC" "DJI"
# 合并收盘价并计算对数收益率
prices <- na.omit(merge(Cl(GSPC), Cl(IXIC), Cl(DJI)))
returns <- na.omit(ROC(prices))
colnames(returns) <- c("SP500", "NASDAQ", "DJI")
# 参数设置
lambda <- 0.94 # 衰减因子
weights <- c(0.5, 0.3, 0.2) # 资产权重向量
portfolio_value <- 1e7 # 组合价值(美元)
conf_level <- 0.95 # 置信水平
# 初始化协方差矩阵
n_assets <- ncol(returns)
n_obs <- nrow(returns)
covar <- array(dim = c(n_assets, n_assets, n_obs))
covar[,,1] <- cov(returns) # 初始协方差矩阵
# 递归更新协方差矩阵
for (i in 2:n_obs) {
r_prev <- as.numeric(returns[i-1, ])
covar[,,i] <- lambda * covar[,,i-1] + (1 - lambda) * outer(r_prev, r_prev)
}
# 计算组合波动率
port_var <- sapply(1:n_obs, function(i) {
t(weights) %*% covar[,,i] %*% weights
})
annual_vol <- sqrt(port_var * 252)
# 计算VaR序列
z_score <- qnorm(conf_level)
VaR_series <- -portfolio_value * z_score * annual_vol
# 输出最新VaR
cat("Latest Portfolio EWMA VaR (95%):",
round(tail(VaR_series, 1), 2), "USD\n")
## Latest Portfolio EWMA VaR (95%): -6013901 USD
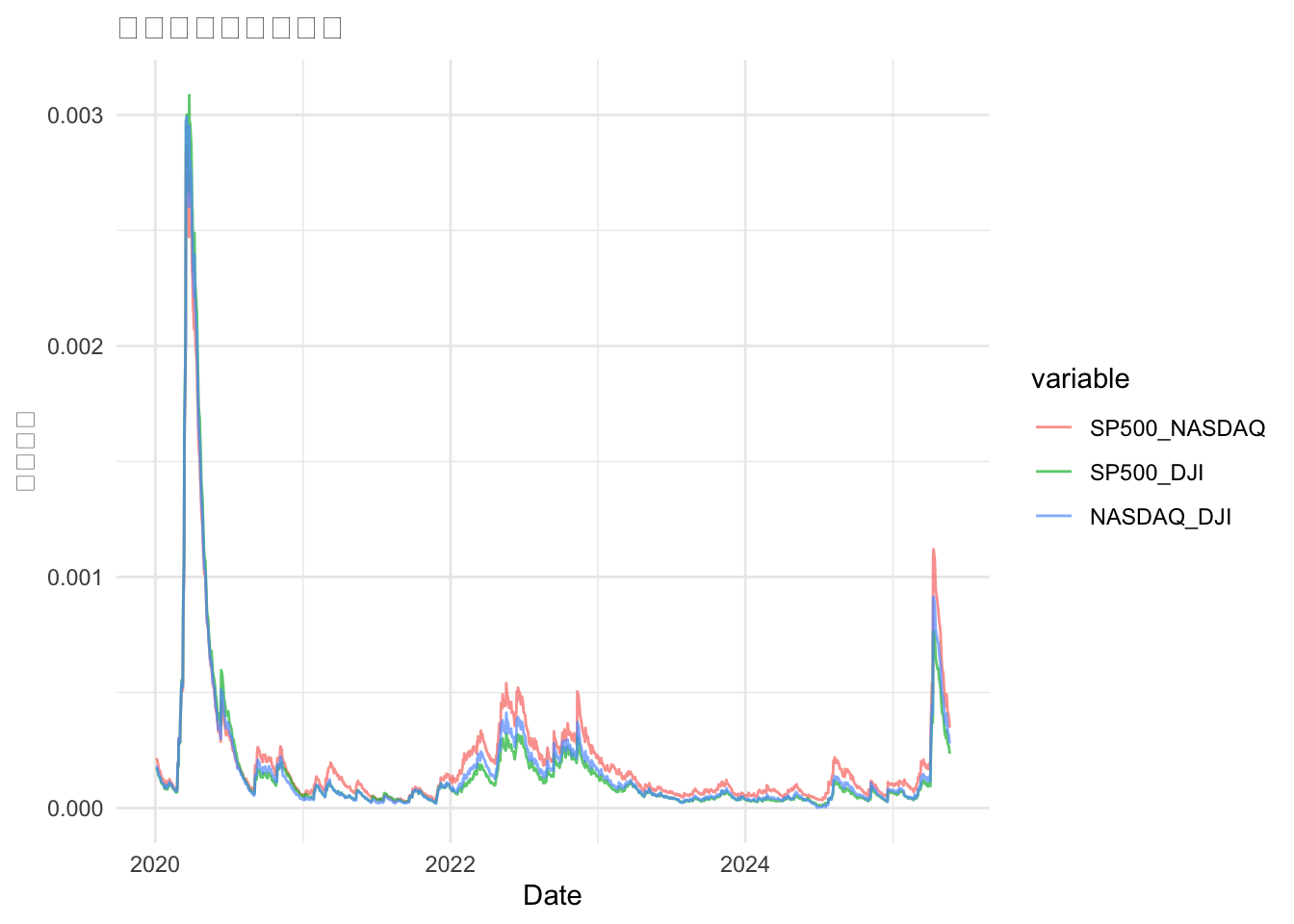
# 可视化协方差矩阵变化
cov_df <- data.frame(
Date = index(returns),
SP500_NASDAQ = sapply(1:n_obs, function(i) covar[1,2,i]),
SP500_DJI = sapply(1:n_obs, function(i) covar[1,3,i]),
NASDAQ_DJI = sapply(1:n_obs, function(i) covar[2,3,i])
)
cov_long <- melt(cov_df, id.vars = "Date")
ggplot(cov_long, aes(x = Date, y = value, color = variable)) +
geom_line(alpha = 0.7) +
labs(title = "协方差动态变化趋势", y = "协方差值") +
theme_minimal()