一、引言

风险价值（Value at Risk, 简称 VaR ）是金融风险管理中衡量市场风险的核心指标，其定义为：在一定置信水平下，某一金融资产或组合在未来特定时间段内可能遭受的最大潜在损失。传统 VaR 计算多假设资产收益率服从正态分布，但实际金融时间序列往往呈现 “尖峰厚尾” 特性（峰度高于正态分布，尾部概率更大），导致正态分布假设下的 VaR 低估尾部风险。

混合正态模型（Mixture of Normals Model）通过将收益率分布拟合为多个正态分布的加权组合，能够有效捕捉尖峰厚尾特征，从而更精准地估计 VaR。

本文详细介绍混合正态模型的构建、参数估计及 VaR 计算方法，并通过 R 语言进行实现。

二、混合正态模型理论模型定义

假设金融资产收益率X服从两成分混合正态分布，其概率密度函数（PDF）为：

\[ f(x; \Theta) = \alpha \cdot \phi(x; \mu_1, \sigma_1^2) + (1-\alpha) \cdot \phi(x; \mu_2, \sigma_2^2) \tag{1} \]

其中：

\(\Theta = (\alpha, \mu_1, \sigma_1^2, \mu_2, \sigma_2^2)\) 为待估参数；

\(\alpha \in (0,1)\) 是第一成分的权重；

\(\phi(x; \mu, \sigma^2) = \frac{1}{\sqrt{2\pi}\sigma} \exp\left(-\frac{(x-\mu)^2}{2\sigma^2}\right)\) 为正态分布密度函数；

\(\mu_1\) , \(\mu_2\) 分别为两成分的均值；

\(\sigma_1^2\) , \(\sigma_2^2\) 分别为两成分的方差。

参数估计

我们可以采用极大似然估计（MLE）求解参数 \(\Theta\) 。设样本观测值为

\[ x_1, x_2, ..., x_n \]

则似然函数为：

\[ L(\Theta) = \prod_{i=1}^n \left[ \alpha \cdot \phi(x_i; \mu_1, \sigma_1^2) + (1-\alpha) \cdot \phi(x_i; \mu_2, \sigma_2^2) \right] \tag{2} \]

取对数似然函数并最大化：

\[ \ln L(\Theta) = \sum_{i=1}^n \ln\left[ \alpha \cdot \phi(x_i; \mu_1, \sigma_1^2) + (1-\alpha) \cdot \phi(x_i; \mu_2, \sigma_2^2) \right] \tag{3} \]

实际求解中，通常采用 EM 算法（期望最大化算法）迭代计算参数估计值。

三、R 语言实证分析

以下通过 R 语言实现基于混合正态模型的 VaR 计算，使用quantmod获取金融数据，mixtools拟合混合正态模型。

1. 加载所需包

# 安装并加载包
if (!require("quantmod")) install.packages("quantmod")
if (!require("mixtools")) install.packages("mixtools")
if (!require("ggplot2")) install.packages("ggplot2")
library(quantmod)
library(mixtools)
library(ggplot2)

2. 获取金融数据并计算收益率

以特斯拉公司的股价为例，计算其对数收益率：

# 获取数据（近5年）
getSymbols("TSLA", from = "2023-01-01", to = "2025-01-01")

## [1] "TSLA"

tsla <- na.omit(Cl(TSLA))  # 提取收盘价并去除缺失值

# 计算对数收益率
returns <- diff(log(tsla))
returns <- na.omit(returns)  # 去除NA值
colnames(returns) <- "收益率"

3. 拟合混合正态模型

使用 mixtools::normalmixEM¹ 拟合两成分混合正态分布：

# 拟合混合正态模型（2个成分）
set.seed(123)  # 设置随机种子，保证结果可复现
mix_model <- normalmixEM(returns, k = 2, maxit = 1000)

## number of iterations= 146

# 输出参数估计结果
cat("混合正态模型参数估计：\n")

## 混合正态模型参数估计：

cat(paste("权重 α =", round(mix_model$lambda[1], 4), "\n"))

## 权重 α = 0.839

cat(paste("成分1：均值 μ1 =", round(mix_model$mu[1], 6), 
          "，标准差 σ1 =", round(mix_model$sigma[1], 6), "\n"))

## 成分1：均值 μ1 = 0.001422 ，标准差 σ1 = 0.027839

cat(paste("成分2：均值 μ2 =", round(mix_model$mu[2], 6), 
          "，标准差 σ2 =", round(mix_model$sigma[2], 6), "\n"))

## 成分2：均值 μ2 = 0.008931 ，标准差 σ2 = 0.063941

4. 定义混合正态分布的 CDF 及 VaR 计算函数

# 混合正态分布的累积分布函数（CDF）
mix_normal_cdf <- function(x, alpha, mu1, sigma1, mu2, sigma2) {
  alpha * pnorm(x, mean = mu1, sd = sigma1) + 
  (1 - alpha) * pnorm(x, mean = mu2, sd = sigma2)
}

# 用二分法求解VaR
var_mixture_normal <- function(conf_level, alpha, mu1, sigma1, mu2, sigma2, data) {
  beta <- 1 - conf_level  # 尾概率
  # 确定搜索区间（基于数据的极值）
  lower <- min(data) * 2
  upper <- 0  # VaR为损失，对应收益率分布的左侧尾部
  # 二分法迭代求解
  for (i in 1:1000) {
    mid <- (lower + upper) / 2
    cdf_val <- mix_normal_cdf(mid, alpha, mu1, sigma1, mu2, sigma2)
    if (cdf_val < beta) {
      lower <- mid
    } else {
      upper <- mid
    }
    if (abs(cdf_val - beta) < 1e-6) break  # 精度满足时停止
  }
  return(-upper)  # 返回VaR（损失值为正）
}

5. 计算 VaR 并与传统方法对比

# 计算95%和99%置信水平下的VaR
conf_levels <- c(0.95, 0.99)
var_results <- sapply(conf_levels, function(cl) {
  var_mixture_normal(conf_level = cl,
                     alpha = mix_model$lambda[1],
                     mu1 = mix_model$mu[1],
                     sigma1 = mix_model$sigma[1],
                     mu2 = mix_model$mu[2],
                     sigma2 = mix_model$sigma[2],
                     data = returns)
})

# 输出VaR结果
cat("\n混合正态模型VaR计算结果：\n")

## 
## 混合正态模型VaR计算结果：

for (i in 1:length(conf_levels)) {
  cat(paste(conf_levels[i] * 100, "%置信水平下的VaR =", 
            round(var_results[i], 6), "\n"))
}

## 95 %置信水平下的VaR = 0.052193 
## 99 %置信水平下的VaR = 0.090665

# 与传统正态分布假设下的VaR对比
var_normal_95 <- quantile(returns, probs = 0.05)  # 正态假设下95% VaR
var_normal_99 <- quantile(returns, probs = 0.01)  # 正态假设下99% VaR
cat("\n传统正态分布假设下的VaR：\n")

## 
## 传统正态分布假设下的VaR：

cat(paste("95%置信水平下的VaR =", round(-as.numeric(var_normal_95), 6), "\n"))

## 95%置信水平下的VaR = 0.051618

cat(paste("99%置信水平下的VaR =", round(-as.numeric(var_normal_99), 6), "\n"))

## 99%置信水平下的VaR = 0.091924

6. 可视化结果

# 绘制收益率分布直方图及混合正态模型拟合曲线
p <- ggplot(data = as.data.frame(returns), aes(x = 收益率)) +
  geom_histogram(aes(y = after_stat(density)), 
                 bins = 50, 
                 fill = "lightblue", 
                 color = "black", 
                 alpha = 0.7) +
  stat_function(fun = function(x) {  # 混合正态模型密度曲线
    mix_model$lambda[1] * dnorm(x, 
                                mean = mix_model$mu[1], 
                                sd = mix_model$sigma[1]) +
    mix_model$lambda[2] * dnorm(x, 
                                mean = mix_model$mu[2], 
                                sd = mix_model$sigma[2])
  }, color = "red", linewidth = 1) +
  geom_vline(xintercept = -var_results[1], 
             color = "blue", 
             linetype = "dashed", 
             linewidth = 1) +
  geom_vline(xintercept = -var_results[2], 
             color = "purple", 
             linetype = "dashed", 
             linewidth = 1) +
  labs(title = "特斯拉收益率分布与混合正态模型拟合",
       x = "对数收益率", y = "密度") +
  theme_minimal()
print(p)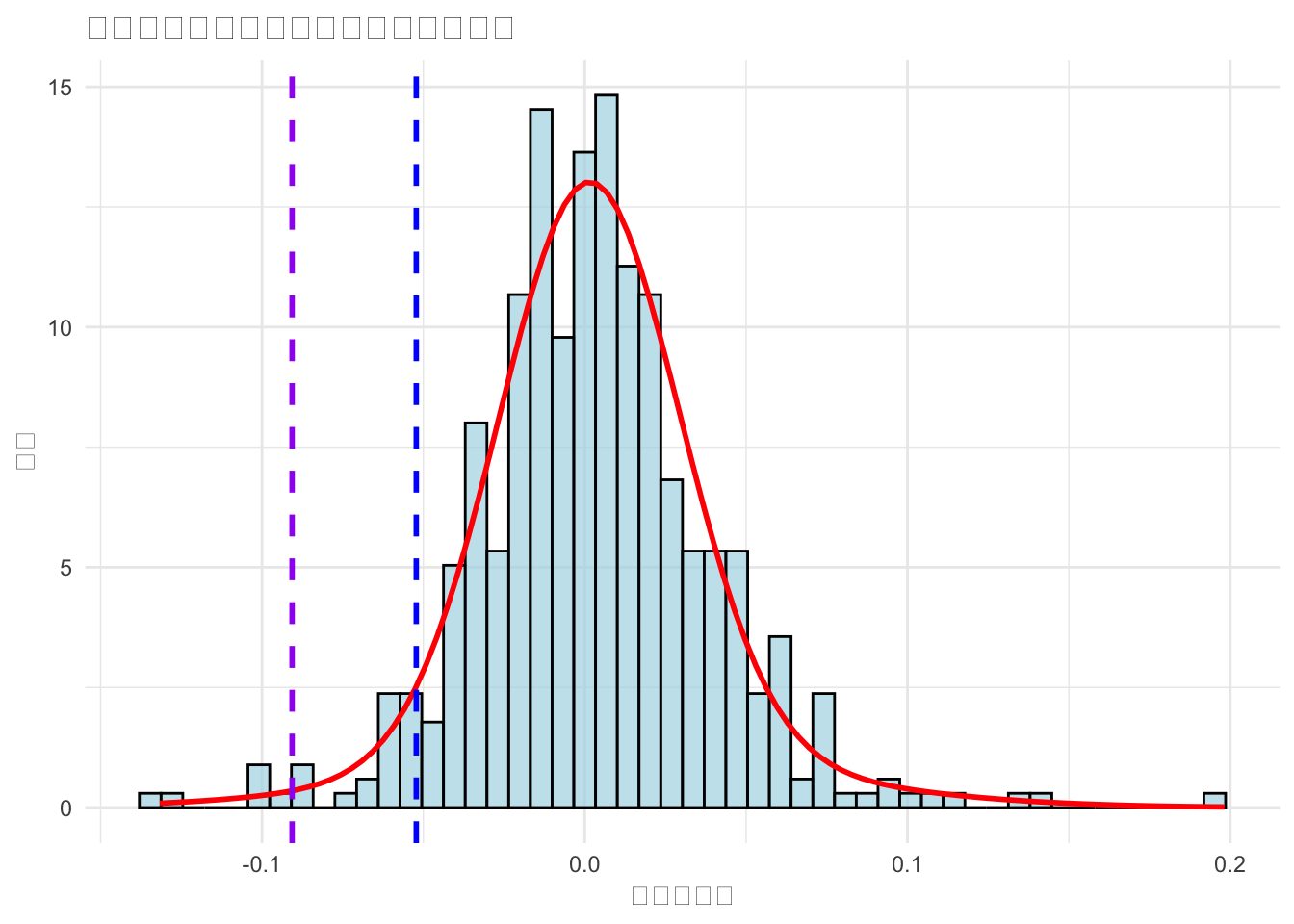

四、结论

混合正态模型通过捕捉金融数据的尖峰厚尾特性，能够更准确地估计 VaR，相比传统正态分布假设更贴合实际风险特征。

实证结果显示，在高置信水平（如 99%）下，混合模型计算的 VaR 通常更高，更能反映极端损失的可能性，为风险管理提供更稳健的参考。实际应用中，可根据数据特征调整混合成分数量（如 3 个成分），或结合其他统计方法（如 GARCH 模型）进一步优化波动率的动态特性。