一、引言
风险价值(VaR)是衡量金融资产潜在损失的核心指标,但传统方法假设收益率服从独立同分布的正态分布,难以捕捉金融时间序列的 “波动聚类”(volatility clustering)和 “尖峰厚尾” 特性。
ARCH(自回归条件异方差)模型及扩展的 GARCH(广义自回归条件异方差)模型通过刻画波动率的动态变化,能更精准地拟合收益率分布,从而提升 VaR 估计的可靠性。
本文以特斯拉(TSLA)股票收益率为例,详细介绍 GARCH 模型的构建、参数估计及 VaR 计算流程,并通过 R 语言quantmod和rgarch包实现实证分析。
二、GARCH 模型理论
ARCH 模型基础
ARCH 模型假设资产收益率的条件方差依赖于过去的平方残差,其核心是波动率的动态性。
均值方程:
\[ r_t = \mu + \epsilon_t \tag{1} \]
其中,
\(r_t\) 为 t 时刻的收益率,
\(\mu\) 为常数均值,
\(\epsilon_t\) 为随机扰动项,且 \(\epsilon_t = \sigma_t \cdot z_t\) ( \(z_t\) )为独立同分布的随机变量,通常假设 \(z_t \sim N(0,1)\) )。
条件方差方程(ARCH (q)):
\[\sigma_t^2 = \omega + \alpha_1 \epsilon_{t-1}^2 + \alpha_2 \epsilon_{t-2}^2 + ... + \alpha_q \epsilon_{t-q}^2 \tag{2} \]
其中,\(\sigma_t^2\) 为 t 时刻的条件方差,\(\omega > 0\) ,\(\alpha_i \geq 0\) (保证方差非负),q为 ARCH 阶数。
GARCH 模型扩展
GARCH 模型在 ARCH 基础上引入过去的条件方差项,简化了高阶 ARCH 模型的参数估计。最常用的 GARCH (p,q) 模型形式为:
均值方程:同式(1)
条件方差方程(GARCH (p,q)):
\[ \sigma_t^2 = \omega + \sum_{i=1}^p \beta_i \sigma_{t-i}^2 + \sum_{j=1}^q \alpha_j \epsilon_{t-j}^2 \tag{3} \]
其中,p为 GARCH 阶数(滞后条件方差项),q为 ARCH 阶数(滞后平方残差项),且 \(\omega > 0\) , \(\beta_i \geq 0\) , \(\alpha_j \geq 0\) , \(\sum_{i=1}^p \beta_i + \sum_{j=1}^q \alpha_j < 1\) (保证方差平稳)。
实际应用中,GARCH (1,1) 模型因简洁且拟合效果好而被广泛使用:
\[ \sigma_t^2 = \omega + \beta_1 \sigma_{t-1}^2 + \alpha_1 \epsilon_{t-1}^2 \tag{4} \]
模型扩展与分布假设变种模型:通过修改条件方差方程可得到 EGARCH(指数 GARCH,捕捉杠杆效应)、IGARCH(积分 GARCH,非平稳波动率)等。
分布假设:为捕捉 “尖峰厚尾”,可假设扰动项 \(z_t\) 服从学生 t 分布(GARCH-t)、广义误差分布(GARCH-GED)等,而非正态分布。
基于 GARCH 模型的 VaR 计算
给定置信水平 \(1-\alpha\) (如 95%、99%),VaR 定义为:
\[ VaR_t = \mu_t + \sigma_t \cdot z_\alpha \tag{5} \]
其中:
\(\mu_t\) 为 t 时刻的条件均值(通常假设为 0 或常数);
\(\sigma_t\) 为 GARCH 模型预测的条件标准差;
\(z_\alpha\) 为扰动项分布的 \(\alpha\) 分位数(如正态分布下 95% 置信水平的 \(z_\alpha = -1.645\) )。
三、R 语言实证分析(TSLA 数据)
- 数据准备与预处理使用 quantmod 获取 TSLA 股票数据并计算对数收益率:
# 安装并加载包
if (!require("quantmod")) install.packages("quantmod")
if (!require("rugarch")) install.packages("rugarch")
if (!require("ggplot2")) install.packages("ggplot2")
library(quantmod)
library(rugarch)
library(ggplot2)
# 获取TSLA数据(2018-2023年)
getSymbols("TSLA", from = "2018-01-01", to = "2023-12-31")## [1] "TSLA"tsla_close <- TSLA$TSLA.Close # 提取收盘价
ret <- diff(log(tsla_close)) # 计算对数收益率
ret <- na.omit(ret) # 去除缺失值
colnames(ret) <- "TSLA_Return"- 拟合 GARCH 模型以 GARCH (1,1) 为例,分别假设正态分布、t 分布和 GED 分布:
# 定义模型规范(正态分布)
garch_spec_norm <- ugarchspec(
variance.model = list(model = "sGARCH", garchOrder = c(1,1)), # 标准GARCH(1,1)
mean.model = list(armaOrder = c(0,0)), # 均值模型为常数(无ARMA项)
distribution.model = "norm" # 正态分布
)
# 拟合模型
garch_fit_norm <- ugarchfit(spec = garch_spec_norm, data = ret)
print(garch_fit_norm) # 输出参数估计结果##
## *---------------------------------*
## * GARCH Model Fit *
## *---------------------------------*
##
## Conditional Variance Dynamics
## -----------------------------------
## GARCH Model : sGARCH(1,1)
## Mean Model : ARFIMA(0,0,0)
## Distribution : norm
##
## Optimal Parameters
## ------------------------------------
## Estimate Std. Error t value Pr(>|t|)
## mu 0.001551 0.000945 1.6407 0.100852
## omega 0.000080 0.000025 3.1932 0.001407
## alpha1 0.066008 0.013489 4.8936 0.000001
## beta1 0.883325 0.026129 33.8057 0.000000
##
## Robust Standard Errors:
## Estimate Std. Error t value Pr(>|t|)
## mu 0.001551 0.001042 1.4883 0.136684
## omega 0.000080 0.000041 1.9324 0.053305
## alpha1 0.066008 0.020564 3.2098 0.001328
## beta1 0.883325 0.040170 21.9898 0.000000
##
## LogLikelihood : 2784.519
##
## Information Criteria
## ------------------------------------
##
## Akaike -3.6877
## Bayes -3.6736
## Shibata -3.6877
## Hannan-Quinn -3.6824
##
## Weighted Ljung-Box Test on Standardized Residuals
## ------------------------------------
## statistic p-value
## Lag[1] 0.02525 0.8737
## Lag[2*(p+q)+(p+q)-1][2] 0.92656 0.5227
## Lag[4*(p+q)+(p+q)-1][5] 2.41996 0.5230
## d.o.f=0
## H0 : No serial correlation
##
## Weighted Ljung-Box Test on Standardized Squared Residuals
## ------------------------------------
## statistic p-value
## Lag[1] 0.06154 0.8041
## Lag[2*(p+q)+(p+q)-1][5] 1.91852 0.6378
## Lag[4*(p+q)+(p+q)-1][9] 3.32230 0.7048
## d.o.f=2
##
## Weighted ARCH LM Tests
## ------------------------------------
## Statistic Shape Scale P-Value
## ARCH Lag[3] 0.1339 0.500 2.000 0.7144
## ARCH Lag[5] 0.1515 1.440 1.667 0.9765
## ARCH Lag[7] 1.3871 2.315 1.543 0.8437
##
## Nyblom stability test
## ------------------------------------
## Joint Statistic: 0.7741
## Individual Statistics:
## mu 0.1583
## omega 0.1017
## alpha1 0.1429
## beta1 0.0778
##
## Asymptotic Critical Values (10% 5% 1%)
## Joint Statistic: 1.07 1.24 1.6
## Individual Statistic: 0.35 0.47 0.75
##
## Sign Bias Test
## ------------------------------------
## t-value prob sig
## Sign Bias 0.1675 0.8670
## Negative Sign Bias 0.3152 0.7527
## Positive Sign Bias 0.5054 0.6134
## Joint Effect 0.4957 0.9198
##
##
## Adjusted Pearson Goodness-of-Fit Test:
## ------------------------------------
## group statistic p-value(g-1)
## 1 20 99.19 7.510e-13
## 2 30 112.84 7.843e-12
## 3 40 122.45 1.505e-10
## 4 50 129.67 3.238e-09
##
##
## Elapsed time : 0.1193922# 扩展:拟合GARCH-t和GARCH-GED
garch_spec_t <- ugarchspec(variance.model = list(model = "sGARCH", garchOrder = c(1,1)),
mean.model = list(armaOrder = c(0,0)),
distribution.model = "std") # 学生t分布
garch_fit_t <- ugarchfit(spec = garch_spec_t, data = ret)
garch_spec_ged <- ugarchspec(variance.model = list(model = "sGARCH", garchOrder = c(1,1)),
mean.model = list(armaOrder = c(0,0)),
distribution.model = "ged") # GED分布
garch_fit_ged <- ugarchfit(spec = garch_spec_ged, data = ret)- 模型参数解读
GARCH (1,1) 模型的核心参数为:
\(\omega\) :常数项(长期方差水平);
\(\alpha_1\) :ARCH 项系数(过去平方残差的影响);
\(\beta_1\) :GARCH 项系数(过去波动率的影响);
若 \(\alpha_1 + \beta_1 < 1\) ,说明波动率平稳。
- 计算 VaR基于拟合模型预测条件波动率,并计算不同置信水平的 VaR:
# 提取条件标准差(在样内预测)
sigma_norm <- sigma(garch_fit_norm) # 正态分布GARCH的条件标准差
# 定义分位数函数(计算z_alpha)
quantile_fun <- function(conf_level, dist) {
alpha <- 1 - conf_level
if (dist == "norm") {
return(qnorm(alpha)) # 正态分布分位数
} else if (dist == "std") {
nu <- coef(garch_fit_t)["shape"] # 学生t分布自由度
return(qt(alpha, df = nu))
} else if (dist == "ged") {
nu <- coef(garch_fit_ged)["shape"] # GED分布形状参数
return(qged(alpha, shape = nu))
}
}
# 计算95%和99%置信水平的VaR(以正态分布为例)
conf_levels <- c(0.95, 0.99)
z_95 <- quantile_fun(0.95, "norm")
z_99 <- quantile_fun(0.99, "norm")
vaR_95_norm <- 0 + sigma_norm * z_95 # 假设条件均值为0
vaR_99_norm <- 0 + sigma_norm * z_99
# 整理结果(取绝对值,损失为正)
vaR_df <- data.frame(
Date = index(ret),
Return = as.numeric(ret),
VaR_95 = abs(vaR_95_norm),
VaR_99 = abs(vaR_99_norm)
)- 结果可视化与回测
# 可视化收益率与VaR
ggplot(vaR_df, aes(x = Date)) +
geom_line(aes(y = Return, color = "收益率"), alpha = 0.7) +
geom_line(aes(y = VaR_95, color = "95% VaR"), linetype = "dashed") +
geom_line(aes(y = VaR_99, color = "99% VaR"), linetype = "dashed") +
labs(title = "TSLA收益率与GARCH模型VaR",
y = "收益率/损失", x = "日期", color = "指标") +
theme_minimal()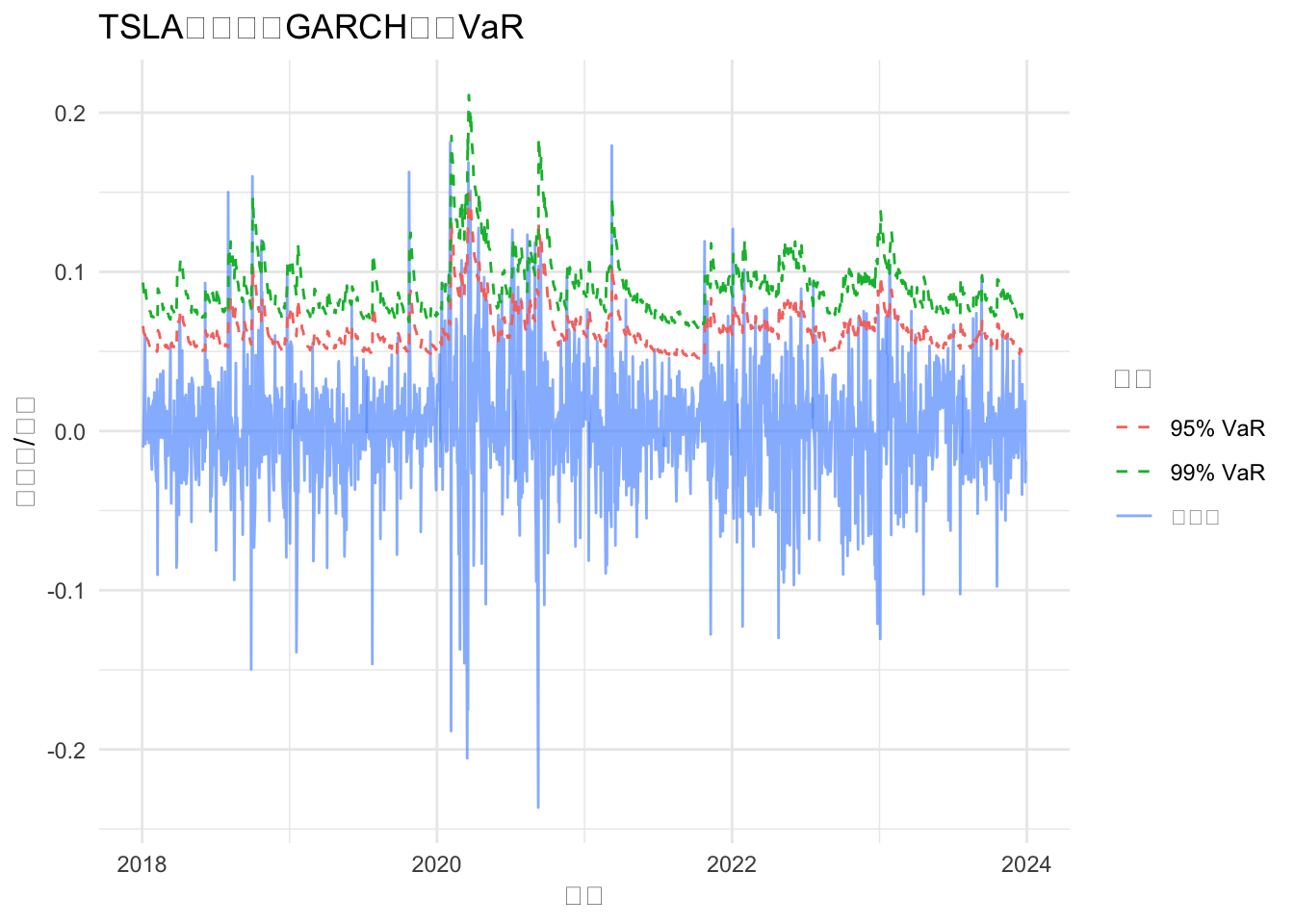
# 回测:计算失败率(实际损失超过VaR的比例)
fail_95 <- mean(vaR_df$Return < -vaR_df$VaR_95, na.rm = TRUE)
fail_99 <- mean(vaR_df$Return < -vaR_df$VaR_99, na.rm = TRUE)
cat("95% VaR失败率:", round(fail_95 * 100, 2), "%\n")## 95% VaR失败率: 4.64 %cat("99% VaR失败率:", round(fail_99 * 100, 2), "%\n")## 99% VaR失败率: 1.59 %- 不同模型的 VaR 对比
可对比 GARCH-t、GARCH-GED 与正态 GARCH 的 VaR 结果,通常非正态分布假设下的 VaR 更大,更保守:
# 计算GARCH-t的VaR(95%置信水平)
sigma_t <- sigma(garch_fit_t)
z_95_t <- quantile_fun(0.95, "std")
vaR_95_t <- abs(sigma_t * z_95_t)四、结论
GARCH 模型通过捕捉波动率的动态变化,显著提升了 VaR 估计的准确性,尤其在市场波动剧烈时期(如 TSLA 股价大幅波动阶段)。
实证显示:TSLA 收益率存在明显的波动聚类特性,GARCH (1,1) 能有效拟合;基于 t 分布或 GED 分布的 GARCH 模型计算的 VaR 更能反映尾部风险,失败率更接近理论置信水平;实际应用中可根据资产特性选择模型变种(如 EGARCH 捕捉杠杆效应)或分布假设。
未来可结合滚动窗口预测或压力测试,进一步优化 VaR 的动态跟踪能力。
注:代码中rugarch包的ugarchspec和ugarchfit函数需注意模型收敛性,若不收敛可调整初始值或模型阶数;回测失败率若显著偏离理论值(如 95% 置信水平下失败率 > 7%),需重新调整模型。