一、引言

风险价值（VaR）作为衡量金融资产极端损失的核心指标，传统方法（如 GARCH 模型）虽能捕捉波动聚类特性，但对尾部风险的刻画仍依赖于整体分布假设。

极值理论（Extreme Value Theory, EVT） 则直接聚焦于收益率序列的尾部行为，通过对极端值建模突破整体分布限制，更精准地估计极端市场条件下的潜在损失。

本文以特斯拉（TSLA）股票收益率为例，系统介绍极值理论的核心模型（广义极值分布 GEV、广义帕累托分布 GPD）、参数估计及 VaR 计算流程，并通过 R 语言fExtremes和evd包实现实证分析。

二、极值理论核心模型

极值理论通过两类方法刻画极端值分布：分块最大值法（Block Maxima Method, BMM） 基于广义极值分布（GEV），超限峰值法（Peaks Over Threshold, POT） 基于广义帕累托分布（GPD）。其中，POT 因灵活利用数据尾部信息而更常用于 VaR 计算。

广义极值分布（GEV）

分块最大值法将时间序列划分为若干块（如按日、周），取每块内的极端值（最大值或最小值），其渐进分布可统一为 GEV。

GEV 分布函数：

\[ G(x; \mu, \sigma, \xi) = \exp\left\{ -\left[1 + \xi \left( \frac{x - \mu}{\sigma} \right) \right]^{-1/\xi} \right\} \tag{1} \]

其中：

\(\mu\) 为位置参数（中心趋势），决定了分布的中心位置，反映极端值的平均水平；
\(\sigma > 0\) 为尺度参数（离散程度）；
\(\xi\) 为形状参数（决定尾部特性）：

若 \(\xi > 0\) ，则 GEV 为 Frechet 分布（厚尾，如幂律尾）。Frechet 分布具有显著的厚尾特征，概率密度函数呈渐近幂律形式，尾部衰减速度较慢，能更准确捕捉金融市场中极端事件发生概率较高的尾部风险，在 VaR 计算中可更可靠地拟合金融资产收益率极端值。

若 \(\xi = 0\) ，则 GEV 为 Gumbel 分布（轻尾，如正态分布）。该分布下极端事件发生概率随偏离均值程度呈指数衰减，数据在均值附近集中程度高，极端值出现频率低，若资产收益符合此分布，表明极端损失发生可能性较小，风险相对可控。

若 \(\xi < 0\) ，则 GEV 为 Weibull 分布（有界尾）。该分布下随机变量存在理论上界，极端事件影响有限，在金融市场中若资产价格波动符合此分布，意味着极端损失幅度有上限，对风险管理者设定止损策略有重要参考价值。

基于 GEV 的 VaR 计算

广义极值分布（GEV）作为统一框架，整合了 Gumbel、Weibull 和 Frechet 三种不同尾部特征的分布类型。基于 GEV 的 VaR 计算，通过极大似然估计或矩估计等方法确定形状参数 \(\xi\) 、位置参数 \(\mu\) 和尺度参数 \(\sigma\) ，构建符合数据尾部特征的风险分布模型。

在给定置信水平 \(1-\alpha\) 下，VaR 为 GEV 分布的 \(\alpha\) 分位数：

\[ VaR_{1-\alpha} = \mu - \frac{\sigma}{\xi} \left[ 1 - (-\ln \alpha)^{-\xi} \right] \quad (\xi \neq 0) \tag{2} \]

广义帕累托分布（GPD）与 POT 方法

POT 方法通过设定阈值 \(u\)，对所有超过 \(u\) 的极端值（超限值）进行建模，其超出量（\(x - u\)）的分布可由广义帕累托分布（Generalized Pareto Distribution，GPD）逼近。

这种方法聚焦于极端事件，能更精准刻画金融市场尾部风险，在金融市场剧烈波动时，可有效捕捉资产价格极端变化，为风险管理者提供重要预警信号，在高风险投资领域应用价值显著。

GPD 分布函数：

广义帕累托分布是刻画超过某一阈值数据分布的重要工具，在金融风险度量中常用于描述极端损失事件概率分布，其概率密度函数为

\[ f(x;\xi,\beta)=\frac{1}{\beta}(1 + \frac{\xi x}{\beta})^{-\frac{1}{\xi}-1} \]

其中 \(x \geq 0\)，\(\beta > 0\) 是尺度参数，\(\xi\) 为形状参数，当 \(\xi = 0\) 时退化为指数分布。

GPD 分布函数为：

\[ F(x;\xi,\beta,\mu)=1-\left(1+\frac{\xi(x - \mu)}{\beta}\right)^{-\frac{1}{\xi}} \]

其中：\(x\geq\mu，1+\frac{\xi(x - \mu)}{\beta}>0\)

其分布函数也可表示为针对超出量的形式：

\[ \begin{cases} 1 - \left(1 + \xi \frac{y}{\sigma}\right)^{-1/\xi} & \xi \neq 0 \\ 1 - \exp\left(-\frac{y}{\sigma}\right) & \xi = 0 \end{cases} \tag{3} \]

其中：

\(y = x - u \geq 0\) 为超出量，代表观测值超过阈值 \(u\) 的部分，反映极端事件偏离阈值的程度。例如，若阈值 \(u\) 设为特斯拉股价单日跌幅 5%，某交易日股价下跌 8% 时，超出量 \(y\) 为 3%。
\(\sigma > 0\) 为尺度参数，决定超出量分布的离散程度。\(\sigma\) 值越大，超出量波动范围越广，投资组合面临的不确定性越高，且其变化与市场宏观环境相关，经济危机期间通常会显著跃升。
\(\xi\) 为形状参数（与 GEV 中的 \(\xi\) 含义相同），\(\xi > 0\) 表示厚尾，直接影响分布尾部厚度与极端事件发生概率估计。\(\xi\) 趋近于 0 时，尾部变薄，极端事件概率降低；\(\xi\) 增大时，极端事件发生可能性显著提升，且在公司重大事件节点往往会出现明显波动。

基于 GPD 的 VaR 计算：

设总样本量为 \(n\)，超限值数量为 \(N_u\)（超限概率 \(\hat{p} = N_u / n\)），则置信水平 \(1-\alpha\) 的 VaR 满足：

\[ 1 - \alpha = (1 - \hat{p}) + \hat{p} \cdot \left[1 - \left(1 + \xi \frac{VaR_{1-\alpha} - u}{\sigma}\right)^{-1/\xi}\right] \tag{4} \]

该公式基于全概率公式推导，将整体风险概率分解为阈值以下和阈值以上两部分。等式左边 \(1 - \alpha\) 为置信水平，右边 \((1 - \hat{p})\) 表示未超过阈值的概率，第二项刻画了阈值以上部分在 GPD 分布下对风险的贡献。如在 95% 置信水平（\(\alpha=0.05\)）下，可据此计算特斯拉股票在极端市场条件下的最大潜在损失。

经代数变换可得：

\[ VaR_{1-\alpha} = u + \frac{\sigma}{\xi} \left[ \left( \frac{n}{N_u} (1 - \alpha) \right)^{-\xi} - 1 \right] \quad (\xi \neq 0) \tag{5} \]

在实际应用中，以特斯拉股价实证分析为例，若总样本量 \(n=1000\) ，超限值数量 \(N_u=50\)，阈值 \(u = 0.03\)，尺度参数 \(\sigma = 0.02\)，形状参数 \(\xi = 0.1\)，在 99% 置信水平下（ \(\alpha = 0.01\) ），代入公式 (5) 计算可得 \(VaR_{0.99} \approx 0.068\)，即特斯拉股票在 99% 置信水平下的单日最大潜在损失约为 6.8%。

此公式为风险管理者提供了定量工具，结合历史数据计算的参数和预设置信水平，可快速得出风险价值，为投资组合配置和止损策略制定提供支持。需注意，当 \(\xi\) 接近 0 时，需采用特殊数值算法确保计算准确性。

阈值选择与模型适用性

阈值的确定：阈值 \(u\) 的选择至关重要，需平衡偏差（ \(u\) 过小导致非极端值混入）与方差（ \(u\) 过大导致样本量不足）。常用的确定方法包括：
- 平均超出量函数（Mean Excess Plot）：绘制超出量均值与阈值 \(u\) 的关系图，寻找超出量均值近似线性的区间。此时的阈值 \(u\) 既能有效分离极端值，又保留足够样本量用于可靠估计。例如分析特斯拉股价数据时，可设定一系列候选阈值，计算对应超出量均值并绘制曲线，选择线性区域内的阈值作为最终 \(u\) 值。
- Hill 图法：计算不同阈值下的 Hill 估计量，绘制其与阈值的关系曲线。随着阈值增加，Hill 估计量应趋于稳定，选取稳定区间内的阈值作为合适的 \(u\) 值，该方法能有效识别复杂尾部特征数据的稳定尾部参数估计区间，增强阈值选择稳健性。
阈值稳定性检验：确保参数 \(\xi\) 和 \(\sigma\) 在 \(u\) 增大时趋于稳定。

三、R 语言实证分析（TSLA 数据）

以 TSLA 股票收益率为例，采用 POT 方法（GPD）计算极端风险 VaR，步骤如下：

1. 数据准备与预处理

使用quantmod获取数据并计算对数收益率（保留损失数据，即负收益率的绝对值）：

# 安装并加载包
if (!require("quantmod")) install.packages("quantmod")
if (!require("fExtremes")) install.packages("fExtremes")
if (!require("evd")) install.packages("evd")
library(quantmod)
library(fExtremes)
library(evd)
library(ggplot2)
library(showtext)
font_add("SimHei","SimHei.ttf")
showtext_auto()
# 获取TSLA数据（2018-2023年）
getSymbols("TSLA", from = "2018-01-01", to = "2023-12-31")

## [1] "TSLA"

tsla_close <- TSLA$TSLA.Close
ret <- diff(log(tsla_close))  # 对数收益率
loss <- -ret  # 损失序列（负收益为损失）
loss <- na.omit(loss)
colnames(loss) <- "TSLA_Loss"

2. 阈值选择（Mean Excess Plot）

通过平均超出量函数确定阈值 \(u\) ：

# 计算平均超出量
u_candidate <- seq(quantile(loss, 0.7), quantile(loss, 0.95), length.out = 20)  # 候选阈值
mean_excess <- sapply(u_candidate, function(u) {
excess <- loss[loss > u] - u  # 超出量
mean(excess, na.rm = TRUE)
})
# 可视化平均超出量
me_df <- data.frame(u = u_candidate, mean_excess = mean_excess)
ggplot(me_df, aes(x = u, y = mean_excess)) +
geom_line(color = "blue") +
geom_point() +
labs(title = "平均超出量函数（确定阈值u）", x = "阈值u", y = "平均超出量") +
theme_minimal()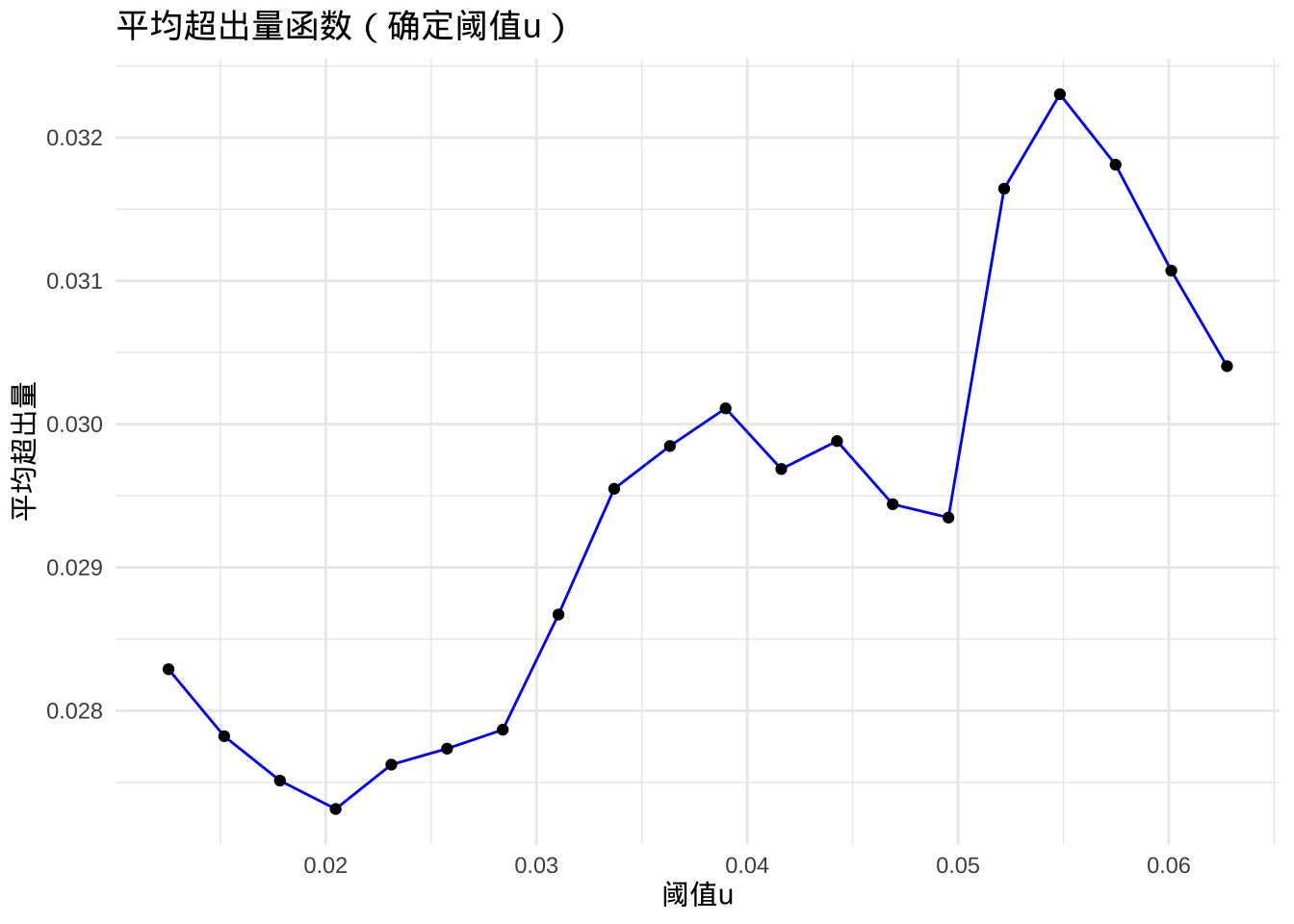

# 选择阈值（如u=0.03，对应约80%分位数）
u <- 0.03
excess <- as.numeric(loss[loss > u] - u)  # 超出量序列

3. GPD 参数估计

使用evd包的fpot函数估计 GPD 的形状参数 \(\xi\) 和尺度参数 \(\sigma\) ：

# 拟合GPD模型
gpd_fit <- fpot(as.numeric(loss), threshold = u)

summary(gpd_fit)  # 输出参数估计结果

##             Length Class  Mode     
## estimate       2   -none- numeric  
## std.err        2   -none- numeric  
## fixed          0   -none- NULL     
## param          2   -none- numeric  
## deviance       1   -none- numeric  
## corr           0   -none- NULL     
## var.cov        4   -none- numeric  
## convergence    1   -none- character
## counts         2   -none- numeric  
## message        0   -none- NULL     
## threshold      1   -none- numeric  
## cmax           1   -none- logical  
## r              0   -none- NULL     
## ulow           1   -none- numeric  
## rlow           1   -none- numeric  
## npp            1   -none- numeric  
## nhigh          1   -none- numeric  
## nat            1   -none- numeric  
## pat            1   -none- numeric  
## extind         0   -none- NULL     
## data        1508   -none- numeric  
## exceedances  244   -none- numeric  
## mper           0   -none- NULL     
## scale          1   -none- numeric  
## call           3   -none- call

# 提取参数

xi <- gpd_fit$estimate["shape"]  # 形状参数ξ

sigma <- gpd_fit$estimate["scale"]  # 尺度参数σ

N <- length(loss)  # 总样本量

Nu <- length(excess)  # 超限值数量

4. 计算 VaR 与回测

基于 GPD 参数计算高置信水平（如 99%、99.5%）的 VaR：

# 定义VaR计算函数（GPD）

calc_evt_var <- function(conf_level, u, xi, sigma, N, Nu) {
alpha <- 1 - conf_level
term <- (N / Nu * alpha)^(-xi)

var <- u + (sigma / xi) * (term - 1)
return(var)

}
# 计算99%和99.5%置信水平的VaR
var_99 <- calc_evt_var(0.99, u, xi, sigma, N, Nu)
var_995 <- calc_evt_var(0.995, u, xi, sigma, N, Nu)
cat("99% VaR（EVT-GPD）：", round(var_99, 4), "\n")

## 99% VaR（EVT-GPD）： 0.1115

cat("99.5% VaR（EVT-GPD）：", round(var_995, 4), "\n")

## 99.5% VaR（EVT-GPD）： 0.1367

# 回测：极端损失超过VaR的比例
extreme_loss <- as.numeric(loss)[loss > u]  # 极端损失序列
fail_99 <- mean(extreme_loss > var_99)
cat("99% VaR失败率：", round(fail_99 * 100, 2), "%\n")

## 99% VaR失败率： 6.15 %

5. 结果可视化

对比实际极端损失与 VaR 阈值：

# 可视化极端损失与VaR
extreme_df <- data.frame(
Date = index(loss)[loss > u],
Extreme_Loss = as.numeric(extreme_loss)
)

ggplot(extreme_df, aes(x = Date, y = Extreme_Loss)) +
geom_point(color = "red") +
geom_hline(yintercept = var_99, 
           color = "blue", 
           linetype = "dashed") +
geom_hline(yintercept = var_995, 
           color = "black", 
           linetype = "dashed") +


labs(title = "TSLA极端损失与EVT-GPD VaR",x = "日期", y = "极端损失（绝对值）") +
theme_minimal()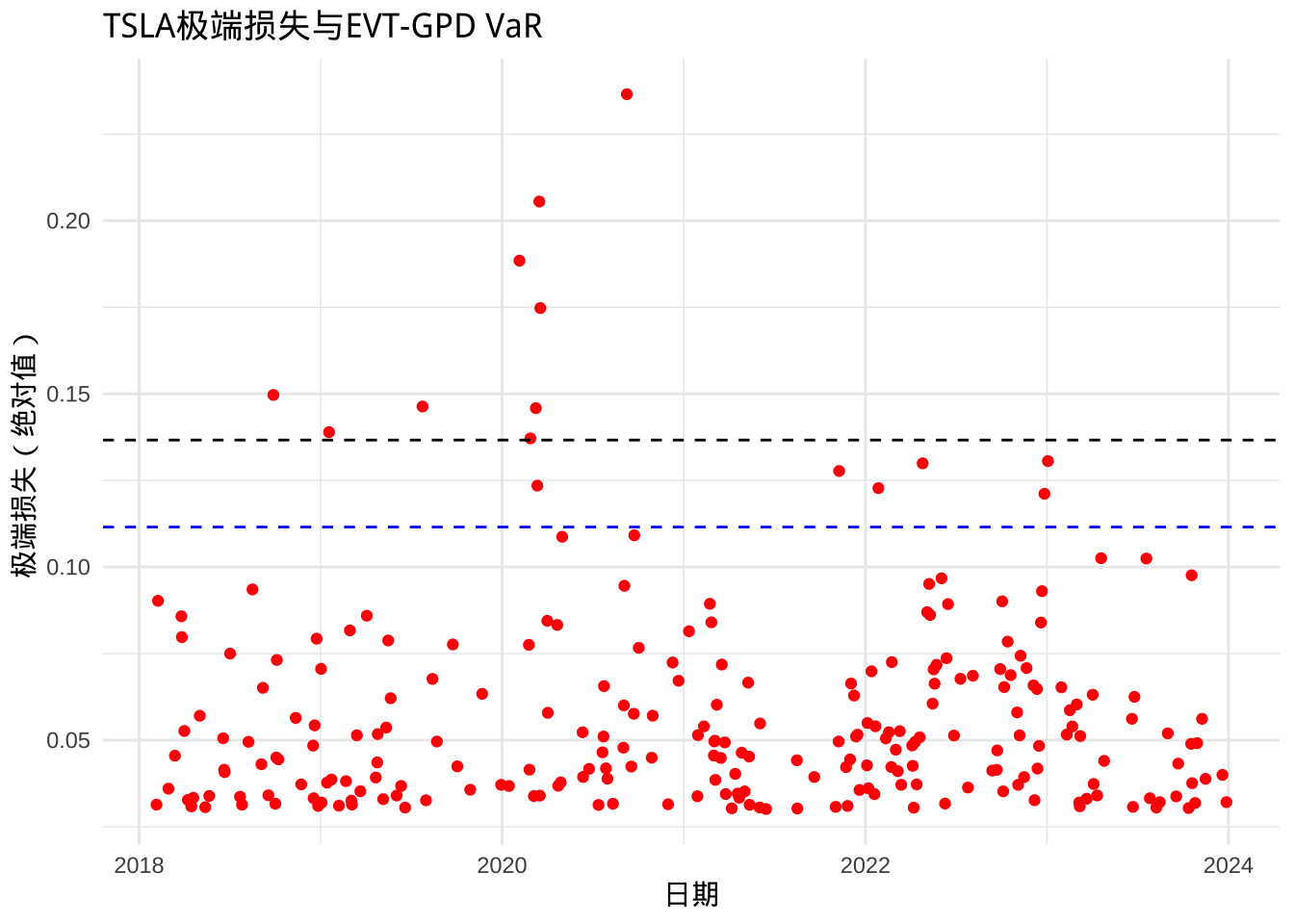

四、结论

极值理论通过直接建模尾部极端值，避免了对整体分布的依赖，在高置信水平下的 VaR 估计更具优势。实证分析显示：

TSLA 股票的极端损失呈现明显厚尾特性（ \(\xi > 0\) ），适合用 GPD 建模；
阈值\(u\)的选择对结果敏感，需结合平均超出量函数和参数稳定性检验确定；
与传统 GARCH 模型相比，EVT 方法计算的高置信水平 VaR 更保守，能更好应对 “黑天鹅” 事件。

未来可结合动态阈值调整或贝叶斯估计，进一步提升 EVT 模型对极端风险的动态跟踪能力。

注：代码中fpot函数需确保阈值\(u\)合理（超限值数量建议占总样本的 5%-10%）；若\(\xi\)接近 0，可简化为指数分布计算 VaR。

基于极值理论的 VaR 计算及实证分析