“协整”算是计量经济学里面的明星概念,不了解计量经济学的人很容易被它笼罩的计量经济学光环给吓到。但事实上,协整并不神秘,是平易近人。
要了解“协整”,首先得提到一个名词——平稳。
什么是平稳时间序列
金融领域有很多类型的时间序列,学者们为了研究的方便通常会对这些时间序列进行分类。比如,按照时间序列数据产生时间间隔的长短分为高频时间序列和非高频时间序列。按照时间序列的平稳性与否,便可以将时间序列分为平稳的时间序列和非平稳的时间序列。
判断某个时间序列平稳与否主要看一下三点:
-
时间序列(随机过程)的均值是否是常数?或者说时间序列(随机过程)的均值是不是跟时间无关?如果不是常数则该时间序列是非平稳的;如果是常数,则该时间序列可能是平稳的,但不肯定,须进入第二步。
-
时间序列(随机过程)的方差是否是常数?或者说时间序列(随机过程)的方差是不是跟时间无关?如果不是常数则该时间序列是非平稳的;如果是常数,则该时间序列可能是平稳的,但不肯定,须进入第三步。
-
任意两个时期的时间序列之间的协方差是否仅仅依赖于两个时间序列的时间间隔。
如果一个时间序列同时满足上述三个条件,那么,该时间序列就是平稳的。
由于均值、方差和协方差可以被统一的成为统计特性,因此也可以说如果时间序列的统计特性不随着时间的推移而发生变化,则说明时间序列是平稳的。
平稳时间序列还可以进一步细分。根据平稳时间序列进行差分的次数,可以将平稳时间序列分为不同阶的平稳时间序列。如果一个时间序列本身是平稳的,那么该时间序列可被记作I(0),括号里面的0表示该时间序列没有进行差分。如果一个时间序列一阶差分之后平稳,那么可被记作I(1),以此类推。
平稳性的检验
在应用过程中,时间序列的平稳性的判断要简单的多。常用的判断时间序列平稳性的方法有两个:图示法和单位根检验法。
图示法,顾名思义,就是画出时间序列的时序图,来目测时间序列是否平稳。如果画出的时间序列不存在明显的趋势,那么时间序列可能是平稳的。这个方法比较随意和主观,因此,只能作为辅助判断的手段。
单位根检验法是一个理论基础扎实的判断手段,单位根检验的方法非常多,一般常用的有DF检验(Dickey-Fuller Test),ADF检验(Augmented Dickey-Fuller Test)和PP检验(Phillips-Perron Test)。这三个检验的理论基础在这里不讲,因为除却数理统计的专业人员,大部分人都不必深究这些理论,现实中只要懂得这些检验用软件的实现方法就可以了。
下面以R为例:
#生成两个时间序列:
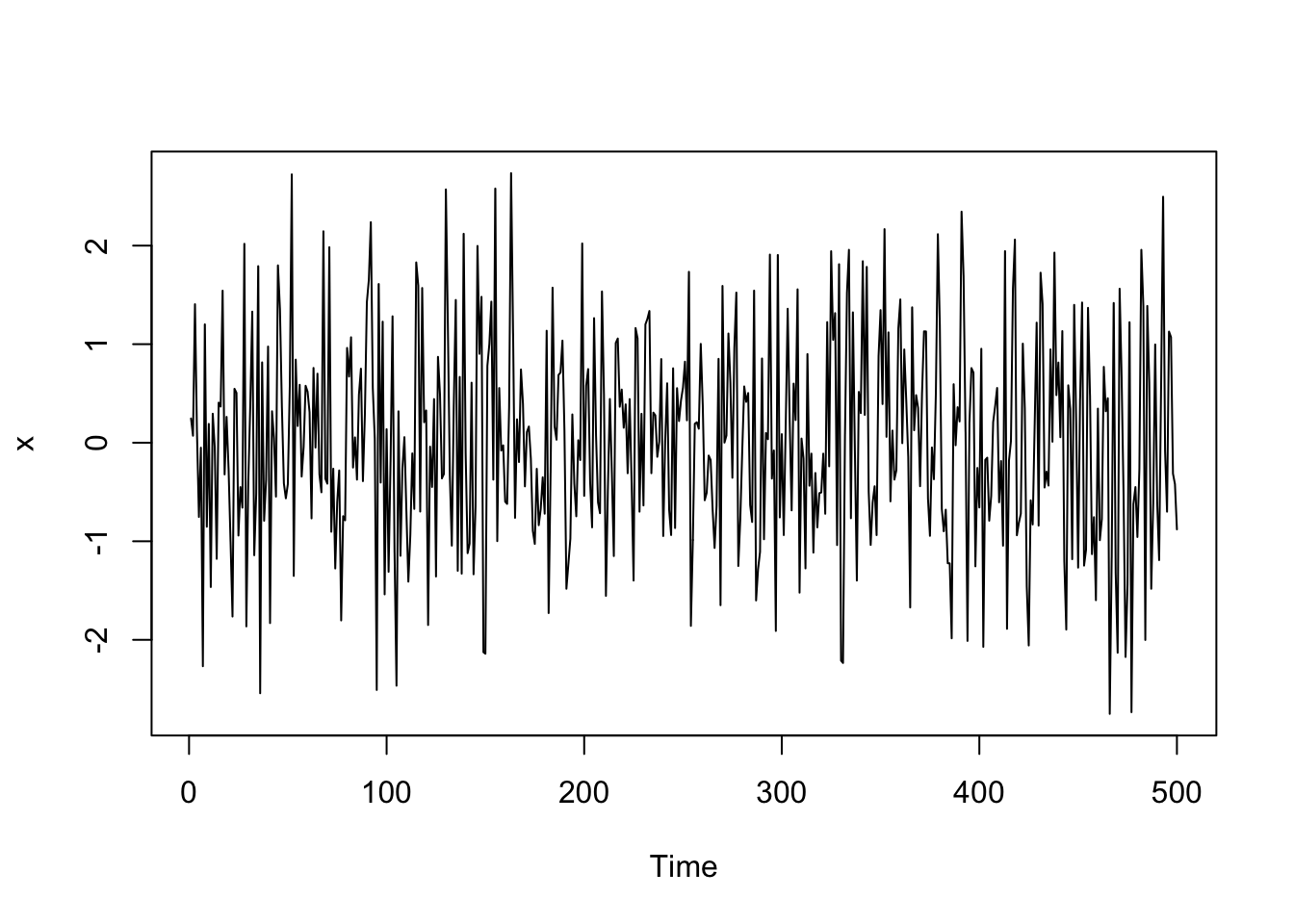
x=rnorm(500); #没有单位根
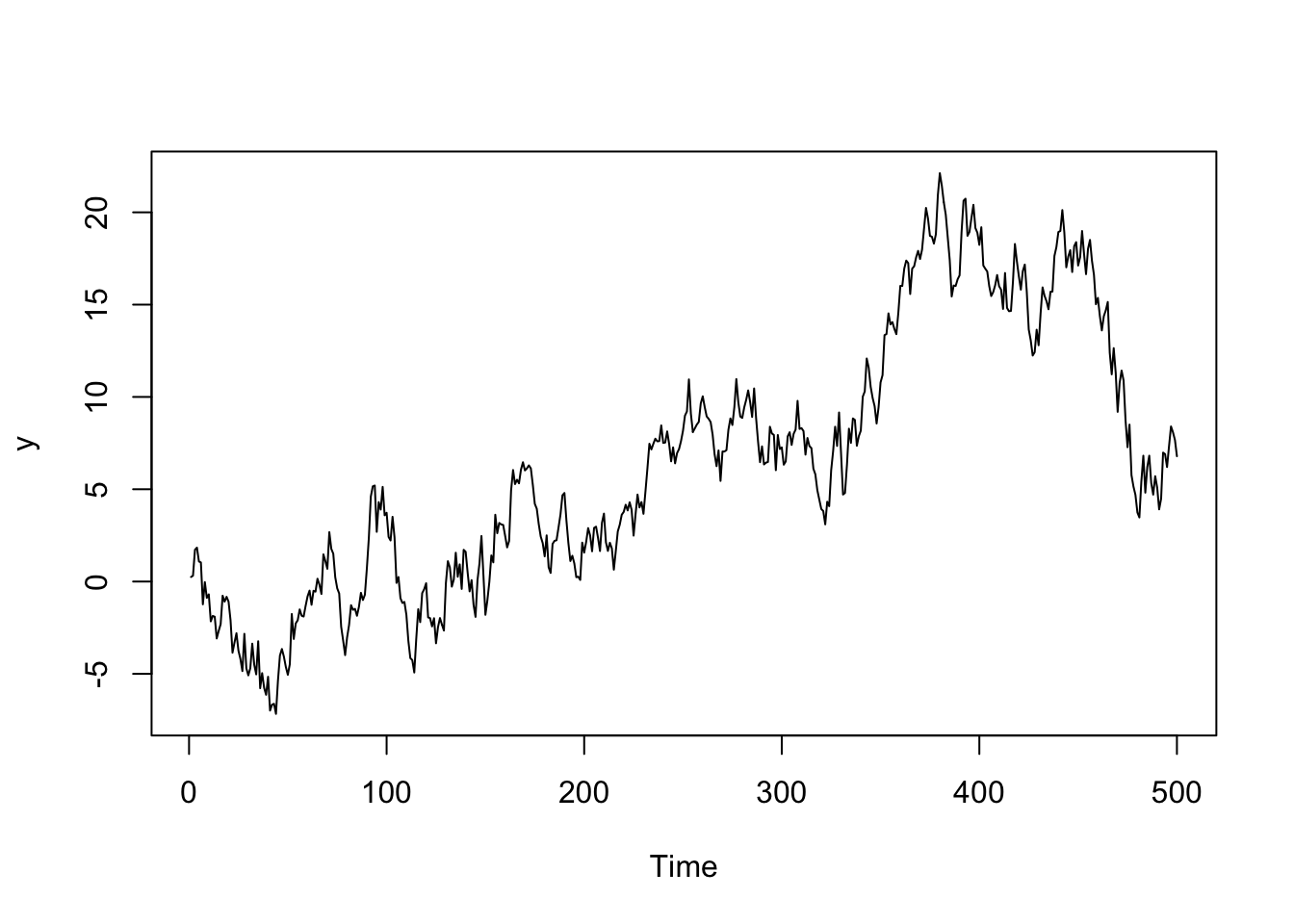
y=cumsum(x); #有单位根
# 绘制时序图
plot.ts(x);
plot.ts(y);
# DF.test检验
library(tseries) #载入tseries包
## Registered S3 method overwritten by 'quantmod':
## method from
## as.zoo.data.frame zoo
adf.test(x)
## Warning in adf.test(x): p-value smaller than printed p-value
##
## Augmented Dickey-Fuller Test
##
## data: x
## Dickey-Fuller = -7.863, Lag order = 7, p-value = 0.01
## alternative hypothesis: stationary
P值等于0.01,拒绝x是原假设(原假设为非平稳),即可以认为x是平稳的。
adf.test(y)
##
## Augmented Dickey-Fuller Test
##
## data: y
## Dickey-Fuller = -2.6979, Lag order = 7, p-value = 0.2829
## alternative hypothesis: stationary
P值等于0.303,因此y是非平稳的。
还可以用urca包中的ur.df()函数来完成上述过程:
# install.packages('urca') #安装urca包
library(urca)#载入urca包
?ur.df#查看ur.df()函数的帮助文档
#用uroot包中的ADF.test()函数来完成上述过程
# install.packages('uroot') #没有安装的话
library(uroot) #载入uroot包
?ADF.test#查看ADF.test()函数的帮助文档
## 在指定的程序包和图书馆里没有与'ADF.test'有关的文档:
## 你可以用用'??ADF.test'
PP检验
library(tseries)
pp.test(x)
## Warning in pp.test(x): p-value smaller than printed p-value
##
## Phillips-Perron Unit Root Test
##
## data: x
## Dickey-Fuller Z(alpha) = -513.04, Truncation lag parameter = 5, p-value
## = 0.01
## alternative hypothesis: stationary
P值等于0.01,拒绝x为非平稳序列的假设。
pp.test(y)
##
## Phillips-Perron Unit Root Test
##
## data: y
## Dickey-Fuller Z(alpha) = -15.795, Truncation lag parameter = 5, p-value
## = 0.2286
## alternative hypothesis: stationary
P值等于0.2056,不能拒绝x是非平稳序列的假设,即x非平稳。
也可以用stats包中的PP.test()函数来完成PP检验。
?PP.test#查看PP.test()函数的帮助文档