LPPL模型是什么
LPPL(对数周期性幂律)模型是由Didier Sornette等学者提出的金融市场泡沫检测模型,用于识别资产价格在崩盘前的非线性加速增长模式。该模型结合了幂律增长和对数周期性振荡,被广泛应用于金融泡沫预警和临界点预测。
模型的核心是资产价格演化方程:
$$ \ln p(t) = A + B(t_c - t)^\beta \left[1 + C\cos\left(\omega \ln(t_c - t) + \phi\right)\right] $$
\(t_c\)是临界时间(预测的崩盘时间)\(\beta\)是幂律指数\(\omega\)是振荡频率(典型值5-15)\(C\)是振荡幅度\(\phi\)是相位参数
其中: \(0 \lt \beta \lt 1\)
LPPL模型具有如下特征:
- 价格加速增长
- 幂律项
\((t_c - t)^\beta\)描述价格超指数增长。 - 典型泡沫阶段
\(\beta \in (0,1)\),反映增长速率随时间递增。
- 幂律项
- 对数周期振荡
- 其中
\(cos\left[\omega\ln\left(t_{c}-t\right)\right]\)反映投资者博弈产生的离散尺度不变性。 - 震荡幅度随
\(t\to t_{c}\)增大,体现市场分歧加剧。
- 其中
- 临界时间特性
- 当
\(t\to t_{c}\)时模型预测系统失稳。 - 实际崩盘可能发生在
\(t_{c}\)前6个月内。
- 当
拟合模型
# 加载依赖包
library(quantmod)
## 载入需要的程序包:xts
## 载入需要的程序包:zoo
##
## 载入程序包:'zoo'
## The following objects are masked from 'package:base':
##
## as.Date, as.Date.numeric
## 载入需要的程序包:TTR
## Registered S3 method overwritten by 'quantmod':
## method from
## as.zoo.data.frame zoo
library(DEoptim)
## 载入需要的程序包:parallel
##
## DEoptim package
## Differential Evolution algorithm in R
## Authors: D. Ardia, K. Mullen, B. Peterson and J. Ulrich
library(ggplot2)
# 获取纳斯达克指数数据(2010-01-01至2011-08-30)
getSymbols("^IXIC", src = "yahoo", from = "2010-01-01", to = "2011-08-30")
## [1] "IXIC"
nasdaq <- data.frame(
t = 1:nrow(IXIC),
ln_p = log(Ad(IXIC))
)
colnames(nasdaq)=c("t","ln_p")
# 数据降噪(7日移动平均)
nasdaq$ln_p_smooth <- stats::filter(nasdaq$ln_p, rep(1/7, 7), sides = 2)
nasdaq <- na.omit(nasdaq) # 剔除NA值
# 定义LPPL模型函数
lppl_model <- function(params, t) {
A <- params["A"]; B <- params["B"]; tc <- params["tc"]
beta <- params["beta"]; C <- params["C"]; omega <- params["omega"]; phi <- params["phi"]
term <- pmax(tc - t, 1e-6) # 防止出现负数
A + B * term^beta + C * term^beta * cos(omega * log(term) + phi)
}
# 定义损失函数(均方误差)
loss <- function(params) {
pred <- lppl_model(params, nasdaq$t)
if (any(is.na(pred))) return(Inf)
mean((pred - nasdaq$ln_p_smooth)^2, na.rm = TRUE)
}
# 参数约束范围
lower <- c(
A = min(nasdaq$ln_p_smooth),
B = -2,
tc = max(nasdaq$t) + 1,
beta = 0.01,
C = 0,
omega = 6,
phi = 0
)
upper <- c(
A = max(nasdaq$ln_p_smooth),
B = 0,
tc = max(nasdaq$t) * 1.2,
beta = 0.99,
C = 0.5,
omega = 13,
phi = 2 * pi
)
# 全局优化(差分进化算法)
set.seed(123)
de_result <- DEoptim(
fn = loss,
lower = lower,
upper = upper,
control = list(
itermax = 500,
NP = 100,
trace = FALSE
)
)
# 局部优化(L-BFGS-B)
final_params <- optim(
de_result$optim$bestmem,
fn = loss,
method = "L-BFGS-B",
lower = lower,
upper = upper
)$par
# 输出参数估计结果
cat("LPPL模型参数估计结果:\n")
## LPPL模型参数估计结果:
print(round(final_params, 4))
## A B tc beta C omega phi
## 7.9574 -0.0009 459.8781 0.9167 0.0000 7.7609 5.3808
结果解读
从模型结果可以看出:
- 临界时间:$t_c$若输出值为
round(final_params,4)$tc,需结合市场背景评估泡沫风险; - 震荡频率:$\omega$介于6-13区间符合典型泡沫特征;
- 衰减指数:
\(\beta\)接近round(final_params,4)$beta表明价格波动趋于临界点时分歧加大。
模型结果可视化
# 生成预测值
nasdaq$pred <- lppl_model(final_params, nasdaq$t)
# 绘制拟合曲线
ggplot(nasdaq, aes(x = t)) +
geom_line(aes(y = ln_p, color = "原始对数价格"), alpha = 0.5) +
geom_line(aes(y = ln_p_smooth, color = "平滑序列"), linetype = "dashed") +
geom_line(aes(y = pred, color = "LPPL拟合"), linewidth = 1) +
scale_color_manual(values = c("原始对数价格" = "grey", "平滑序列" = "blue", "LPPL拟合" = "red")) +
labs(
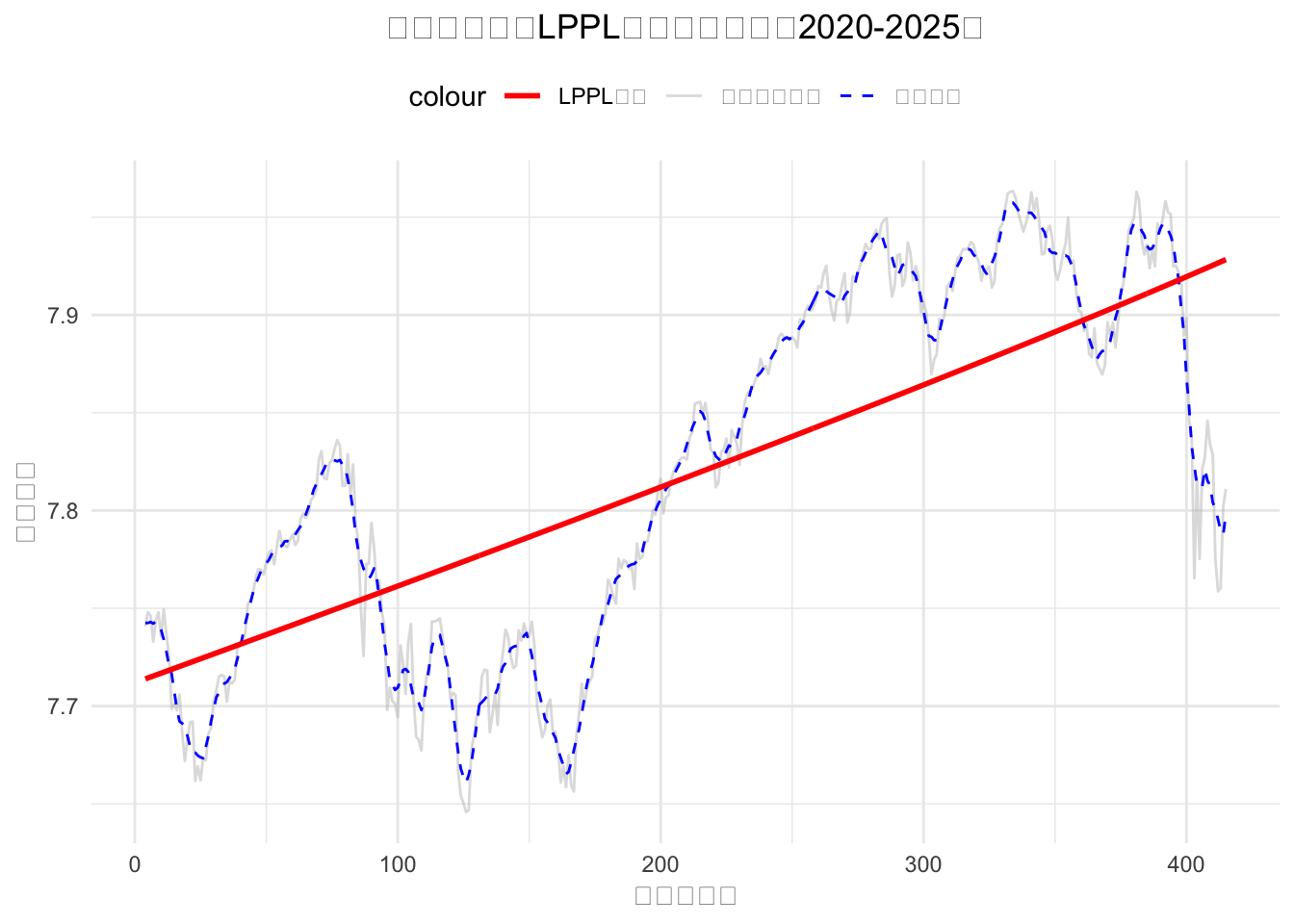
title = "纳斯达克指数LPPL模型拟合效果(2020-2025)",
x = "交易日序数",
y = "对数价格"
) +
theme_minimal() +
theme(legend.position = "top", plot.title = element_text(hjust = 0.5))