摘要

本文运用 Log-Periodic Power Law (LPPL) 模型对纳斯达克指数进行分析，旨在识别市场中的泡沫特征并预测潜在的趋势转折点。LPPL 模型结合了幂律和对数周期振荡，能够捕捉金融市场中的非线性特征和临界现象。

通过 R 语言实现模型拟合与参数估计，我们对纳斯达克指数在不同历史时期的泡沫形成与破裂过程进行了实证研究，并验证了模型在市场极端波动情况下的应用价值。

LPPL 模型理论基础

LPPL 模型由 Didier Sornette 提出的一种用于描述金融市场泡沫和崩溃的数学模型，其核心思想是将价格的加速上涨（或下跌）与对数周期性振荡相结合，反映市场参与者的从众心理和正反馈机制。

LPPL 模型的数学表达式为：

\[ \ln P(t) = A + B(t_c - t)^\beta + C(t_c - t)^\beta \cos\left[\omega \ln(t_c - t) + \phi\right] \]

其中：

\(P(t)\) 是资产价格
\(t_c\) 是临界时间点（泡沫破裂的理论时间）
\(\beta\) 是幂律指数（ \(0 < \beta < 1\) ），控制价格加速上涨的速率
\(\omega\) 是振荡频率，控制对数周期振荡的周期
\(\phi\) 是相位角，控制振荡的起始位置
\(A, B, C\) 是常数参数，分别表示价格基准水平、趋势方向和振荡幅度

模型各部分的经济学解释

幂律部分 \(B(t_c - t)^\beta\) :

加速特征：当 t 趋近于 \(t_c\) 时，\((t_c - t)^\beta\) 趋近于 0，但由于 \(\beta < 1\)，其导数会趋向无穷大，导致价格加速上涨（若 \(\beta<0\) 则为加速下跌）。
市场含义：反映投资者的从众心理和正反馈机制，随着泡沫接近破裂，价格变化速率不断加快。

对数周期振荡部分 \(C(t_c - t)^\beta \cos\left[\omega \ln(t_c - t) + \phi\right]\) ：

对数周期性：振荡频率随时间对数变化，表现为周期逐渐缩短的波动。
市场含义：反映市场参与者的情绪波动和多空博弈。随着临界时间点临近，投资者对泡沫破裂的预期增强，导致市场波动加剧且周期变短。

模型中的参数都有明确的经济学意义。其中，\(t_c\) 表示模型预测的泡沫破裂时间点；\(\beta\) 反映市场的脆弱性，\(\beta\) 越小表示价格加速越快，泡沫越脆弱；\(\omega\) 与市场参与者的群体行为周期相关，较高的 \(\omega\) 表示市场情绪波动更频繁。

估计模型参数

估计 LPPL 模型的核心是通过历史价格数据找到一组参数 \(\{A, B, C, \beta, \omega, \phi, t_c\}\)，使得模型预测值与实际价格的拟合误差最小化。这通常通过以下步骤实现：

目标函数构建

定义残差平方和（SSE）作为目标函数：

\[ \text{SSE} = \sum_{i=1}^N \left[ \ln P(t_i) - \left( A + B(t_c - t_i)^\beta + C(t_c - t_i)^\beta \cos\left(\omega \ln(t_c - t_i) + \phi\right) \right) \right]^2 \]

其中 \(P(t_i)\) 是实际价格，\(N\) 是样本量。

由于 LPPL 模型是非线性的，且参数之间存在复杂的相互作用，通常使用全局优化算法求解，如：

差分进化算法（DE）：在 R 代码中使用的 DEoptim 包即基于此算法
遗传算法（GA）
模拟退火算法

为确保参数的合理性，还需设置对参数的约束条件，具体如下：

\(t_c > \text{当前时间}\) ：临界时间必须在未来
\(0 < \beta < 1\) ：确保幂律部分的加速特性
\(\omega > 2\pi\) ：确保存在足够的振荡周期
\(A > 0\) ：确保对数价格有意义

由于模型包含对数和幂指数运算，当 t 接近 \(t_c\) 时容易出现数值溢出或下溢。在实际计算中，通常需要：

对 \(t_c - t\) 设置最小值（如 1e-10）。
对结果设置合理的上下限。
在对数空间进行计算，再转换回价格空间。

R 语言实现 LPPL 模型分析

下面是使用 R 语言实现 LPPL 模型分析纳斯达克指数的完整代码：

# 加载必要的包
library(quantmod)
library(DEoptim)
library(ggplot2)
library(reshape2)
library(showtext)
font_add("SimHei", regular="SimHei.ttf")
showtext_auto()

# 获取纳斯达克指数数据
getSymbols("^IXIC", from = "2024-01-01", to = Sys.Date())

## [1] "IXIC"

nasdaq <- IXIC$IXIC.Close
names(nasdaq) <- "Close"

# 数据预处理
prices <- as.numeric(nasdaq)
dates <- index(nasdaq)
t <- seq_along(prices)

# LPPL模型函数（优化数值稳定性）
lppl <- function(t, tc, beta, omega, phi, A, B, C) {
  safe_diff <- pmax(tc - t, 1e-10)
  power_term <- safe_diff^beta
  cos_term <- cos(omega * log(safe_diff) + phi)
  result <- A + B * power_term + C * power_term * cos_term
  result <- pmax(pmin(result, 20), -20)
  return(result)
}

# 残差平方和函数
lppl_sse <- function(params, t, y) {
  tc <- params[1]
  beta <- params[2]
  omega <- params[3]
  phi <- params[4]
  A <- params[5]
  B <- params[6]
  C <- params[7]
  
  if (tc <= max(t) + 1 || beta <= 0 || beta >= 1 || omega <= 0 || A < 0) {
    return(1e10)
  }
  
  y_pred <- lppl(t, tc, beta, omega, phi, A, B, C)
  sum((log(y) - y_pred)^2)
}

# 定义参数优化边界
lower <- c(max(t) + 5, 0.1, 2 * pi, 0, min(log(prices)), -100, -100)
upper <- c(max(t) + 365, 0.9, 10 * pi, 2 * pi, max(log(prices)), 100, 100)

# 差分进化算法优化
set.seed(123)
result <- DEoptim(lppl_sse, lower, upper,
                  control = list(itermax = 200, NP = 100, strategy = 2, trace = TRUE),
                  t = t, y = prices)

## Iteration: 1 bestvalit: 39895.714279 bestmemit:  476.249449    0.558294   18.948798    5.937831    9.814416   68.908510  -38.291566
## Iteration: 2 bestvalit: 29497.840447 bestmemit:  434.050449    0.319333   13.766252    6.139294    9.924482    5.318016   -6.565053
## Iteration: 3 bestvalit: 29497.840447 bestmemit:  434.050449    0.319333   13.766252    6.139294    9.924482    5.318016   -6.565053
## Iteration: 4 bestvalit: 29497.840447 bestmemit:  434.050449    0.319333   13.766252    6.139294    9.924482    5.318016   -6.565053
## Iteration: 5 bestvalit: 29497.840447 bestmemit:  434.050449    0.319333   13.766252    6.139294    9.924482    5.318016   -6.565053
## Iteration: 6 bestvalit: 29497.840447 bestmemit:  434.050449    0.319333   13.766252    6.139294    9.924482    5.318016   -6.565053
## Iteration: 7 bestvalit: 29497.840447 bestmemit:  434.050449    0.319333   13.766252    6.139294    9.924482    5.318016   -6.565053
## Iteration: 8 bestvalit: 29497.840447 bestmemit:  434.050449    0.319333   13.766252    6.139294    9.924482    5.318016   -6.565053
## Iteration: 9 bestvalit: 29497.840447 bestmemit:  434.050449    0.319333   13.766252    6.139294    9.924482    5.318016   -6.565053
## Iteration: 10 bestvalit: 27066.806727 bestmemit:  651.029055    0.151405    8.772378    0.740875    9.824145    6.663771   -5.323786
## Iteration: 11 bestvalit: 27066.806727 bestmemit:  651.029055    0.151405    8.772378    0.740875    9.824145    6.663771   -5.323786
## Iteration: 12 bestvalit: 27066.806727 bestmemit:  651.029055    0.151405    8.772378    0.740875    9.824145    6.663771   -5.323786
## Iteration: 13 bestvalit: 27066.806727 bestmemit:  651.029055    0.151405    8.772378    0.740875    9.824145    6.663771   -5.323786
## Iteration: 14 bestvalit: 11955.860681 bestmemit:  435.863572    0.143216   22.799105    0.221635    9.753128   -2.266998    1.829183
## Iteration: 15 bestvalit: 11955.860681 bestmemit:  435.863572    0.143216   22.799105    0.221635    9.753128   -2.266998    1.829183
## Iteration: 16 bestvalit: 11955.860681 bestmemit:  435.863572    0.143216   22.799105    0.221635    9.753128   -2.266998    1.829183
## Iteration: 17 bestvalit: 4159.769617 bestmemit:  435.863572    0.143216   22.232637    4.730370    9.767731    0.690221    1.829183
## Iteration: 18 bestvalit: 4159.769617 bestmemit:  435.863572    0.143216   22.232637    4.730370    9.767731    0.690221    1.829183
## Iteration: 19 bestvalit: 4159.769617 bestmemit:  435.863572    0.143216   22.232637    4.730370    9.767731    0.690221    1.829183
## Iteration: 20 bestvalit: 4159.769617 bestmemit:  435.863572    0.143216   22.232637    4.730370    9.767731    0.690221    1.829183
## Iteration: 21 bestvalit: 4159.769617 bestmemit:  435.863572    0.143216   22.232637    4.730370    9.767731    0.690221    1.829183
## Iteration: 22 bestvalit: 4135.691142 bestmemit:  435.863572    0.143216   15.614739    1.345954    9.767731    0.690221    1.829183
## Iteration: 23 bestvalit: 4135.691142 bestmemit:  435.863572    0.143216   15.614739    1.345954    9.767731    0.690221    1.829183
## Iteration: 24 bestvalit: 4135.691142 bestmemit:  435.863572    0.143216   15.614739    1.345954    9.767731    0.690221    1.829183
## Iteration: 25 bestvalit: 4135.691142 bestmemit:  435.863572    0.143216   15.614739    1.345954    9.767731    0.690221    1.829183
## Iteration: 26 bestvalit: 3966.594960 bestmemit:  470.360050    0.143216   15.614739    1.345954    9.767731    0.690221    1.829183
## Iteration: 27 bestvalit: 3966.594960 bestmemit:  470.360050    0.143216   15.614739    1.345954    9.767731    0.690221    1.829183
## Iteration: 28 bestvalit: 3966.594960 bestmemit:  470.360050    0.143216   15.614739    1.345954    9.767731    0.690221    1.829183
## Iteration: 29 bestvalit: 3966.594960 bestmemit:  470.360050    0.143216   15.614739    1.345954    9.767731    0.690221    1.829183
## Iteration: 30 bestvalit: 3966.594960 bestmemit:  470.360050    0.143216   15.614739    1.345954    9.767731    0.690221    1.829183
## Iteration: 31 bestvalit: 3966.594960 bestmemit:  470.360050    0.143216   15.614739    1.345954    9.767731    0.690221    1.829183
## Iteration: 32 bestvalit: 3966.594960 bestmemit:  470.360050    0.143216   15.614739    1.345954    9.767731    0.690221    1.829183
## Iteration: 33 bestvalit: 3966.594960 bestmemit:  470.360050    0.143216   15.614739    1.345954    9.767731    0.690221    1.829183
## Iteration: 34 bestvalit: 3966.594960 bestmemit:  470.360050    0.143216   15.614739    1.345954    9.767731    0.690221    1.829183
## Iteration: 35 bestvalit: 3707.731173 bestmemit:  470.360050    0.143216   15.614739    3.844729    9.767731    0.690221    1.829183
## Iteration: 36 bestvalit: 1346.903100 bestmemit:  404.762508    0.155723   16.208832    1.750229    9.819536   -0.842073    0.071061
## Iteration: 37 bestvalit: 1346.903100 bestmemit:  404.762508    0.155723   16.208832    1.750229    9.819536   -0.842073    0.071061
## Iteration: 38 bestvalit: 1346.903100 bestmemit:  404.762508    0.155723   16.208832    1.750229    9.819536   -0.842073    0.071061
## Iteration: 39 bestvalit: 1346.903100 bestmemit:  404.762508    0.155723   16.208832    1.750229    9.819536   -0.842073    0.071061
## Iteration: 40 bestvalit: 1346.903100 bestmemit:  404.762508    0.155723   16.208832    1.750229    9.819536   -0.842073    0.071061
## Iteration: 41 bestvalit: 1346.903100 bestmemit:  404.762508    0.155723   16.208832    1.750229    9.819536   -0.842073    0.071061
## Iteration: 42 bestvalit: 1279.262391 bestmemit:  404.762508    0.155723   16.808283    5.145210    9.862787   -0.842073    0.071061
## Iteration: 43 bestvalit: 1279.262391 bestmemit:  404.762508    0.155723   16.808283    5.145210    9.862787   -0.842073    0.071061
## Iteration: 44 bestvalit: 1279.262391 bestmemit:  404.762508    0.155723   16.808283    5.145210    9.862787   -0.842073    0.071061
## Iteration: 45 bestvalit: 1279.262391 bestmemit:  404.762508    0.155723   16.808283    5.145210    9.862787   -0.842073    0.071061
## Iteration: 46 bestvalit: 1252.379043 bestmemit:  404.762508    0.155723   18.245900    5.145210    9.862787   -0.842073    0.071061
## Iteration: 47 bestvalit: 1252.379043 bestmemit:  404.762508    0.155723   18.245900    5.145210    9.862787   -0.842073    0.071061
## Iteration: 48 bestvalit: 1252.379043 bestmemit:  404.762508    0.155723   18.245900    5.145210    9.862787   -0.842073    0.071061
## Iteration: 49 bestvalit: 1252.379043 bestmemit:  404.762508    0.155723   18.245900    5.145210    9.862787   -0.842073    0.071061
## Iteration: 50 bestvalit: 36.028168 bestmemit:  459.046057    0.115371   23.997670    2.837452    9.858859   -0.186635    0.077161
## Iteration: 51 bestvalit: 36.028168 bestmemit:  459.046057    0.115371   23.997670    2.837452    9.858859   -0.186635    0.077161
## Iteration: 52 bestvalit: 35.907156 bestmemit:  459.046057    0.115371   23.997670    3.006606    9.858859   -0.186635    0.077161
## Iteration: 53 bestvalit: 35.907156 bestmemit:  459.046057    0.115371   23.997670    3.006606    9.858859   -0.186635    0.077161
## Iteration: 54 bestvalit: 35.907156 bestmemit:  459.046057    0.115371   23.997670    3.006606    9.858859   -0.186635    0.077161
## Iteration: 55 bestvalit: 35.907156 bestmemit:  459.046057    0.115371   23.997670    3.006606    9.858859   -0.186635    0.077161
## Iteration: 56 bestvalit: 35.907156 bestmemit:  459.046057    0.115371   23.997670    3.006606    9.858859   -0.186635    0.077161
## Iteration: 57 bestvalit: 35.907156 bestmemit:  459.046057    0.115371   23.997670    3.006606    9.858859   -0.186635    0.077161
## Iteration: 58 bestvalit: 35.907156 bestmemit:  459.046057    0.115371   23.997670    3.006606    9.858859   -0.186635    0.077161
## Iteration: 59 bestvalit: 34.377659 bestmemit:  428.703249    0.115371   23.997670    3.006606    9.858859   -0.186635    0.077161
## Iteration: 60 bestvalit: 31.613471 bestmemit:  462.969626    0.105108   23.997670    3.006606    9.858859   -0.186635    0.077161
## Iteration: 61 bestvalit: 31.613471 bestmemit:  462.969626    0.105108   23.997670    3.006606    9.858859   -0.186635    0.077161
## Iteration: 62 bestvalit: 31.613471 bestmemit:  462.969626    0.105108   23.997670    3.006606    9.858859   -0.186635    0.077161
## Iteration: 63 bestvalit: 31.613471 bestmemit:  462.969626    0.105108   23.997670    3.006606    9.858859   -0.186635    0.077161
## Iteration: 64 bestvalit: 31.613471 bestmemit:  462.969626    0.105108   23.997670    3.006606    9.858859   -0.186635    0.077161
## Iteration: 65 bestvalit: 31.424669 bestmemit:  462.969626    0.105108   23.997670    3.185548    9.858859   -0.186635    0.077161
## Iteration: 66 bestvalit: 31.323268 bestmemit:  462.969626    0.105108   23.997670    3.274915    9.858859   -0.186635    0.077161
## Iteration: 67 bestvalit: 31.323268 bestmemit:  462.969626    0.105108   23.997670    3.274915    9.858859   -0.186635    0.077161
## Iteration: 68 bestvalit: 31.323268 bestmemit:  462.969626    0.105108   23.997670    3.274915    9.858859   -0.186635    0.077161
## Iteration: 69 bestvalit: 26.740039 bestmemit:  462.969626    0.105108   23.997670    3.274915    9.883282   -0.186635    0.077161
## Iteration: 70 bestvalit: 26.740039 bestmemit:  462.969626    0.105108   23.997670    3.274915    9.883282   -0.186635    0.077161
## Iteration: 71 bestvalit: 26.740039 bestmemit:  462.969626    0.105108   23.997670    3.274915    9.883282   -0.186635    0.077161
## Iteration: 72 bestvalit: 26.740039 bestmemit:  462.969626    0.105108   23.997670    3.274915    9.883282   -0.186635    0.077161
## Iteration: 73 bestvalit: 26.740039 bestmemit:  462.969626    0.105108   23.997670    3.274915    9.883282   -0.186635    0.077161
## Iteration: 74 bestvalit: 26.740039 bestmemit:  462.969626    0.105108   23.997670    3.274915    9.883282   -0.186635    0.077161
## Iteration: 75 bestvalit: 26.740039 bestmemit:  462.969626    0.105108   23.997670    3.274915    9.883282   -0.186635    0.077161
## Iteration: 76 bestvalit: 26.740039 bestmemit:  462.969626    0.105108   23.997670    3.274915    9.883282   -0.186635    0.077161
## Iteration: 77 bestvalit: 26.740039 bestmemit:  462.969626    0.105108   23.997670    3.274915    9.883282   -0.186635    0.077161
## Iteration: 78 bestvalit: 23.060592 bestmemit:  566.173679    0.106387   30.107988    4.119188    9.782746    0.110396    0.063190
## Iteration: 79 bestvalit: 23.060592 bestmemit:  566.173679    0.106387   30.107988    4.119188    9.782746    0.110396    0.063190
## Iteration: 80 bestvalit: 23.060592 bestmemit:  566.173679    0.106387   30.107988    4.119188    9.782746    0.110396    0.063190
## Iteration: 81 bestvalit: 8.540436 bestmemit:  462.969626    0.105108   23.997670    3.274915    9.883282   -0.015204    0.077161
## Iteration: 82 bestvalit: 8.540436 bestmemit:  462.969626    0.105108   23.997670    3.274915    9.883282   -0.015204    0.077161
## Iteration: 83 bestvalit: 8.540436 bestmemit:  462.969626    0.105108   23.997670    3.274915    9.883282   -0.015204    0.077161
## Iteration: 84 bestvalit: 8.540436 bestmemit:  462.969626    0.105108   23.997670    3.274915    9.883282   -0.015204    0.077161
## Iteration: 85 bestvalit: 8.540436 bestmemit:  462.969626    0.105108   23.997670    3.274915    9.883282   -0.015204    0.077161
## Iteration: 86 bestvalit: 8.058381 bestmemit:  653.124574    0.112853   20.292797    1.503638    9.843571   -0.023273    0.055355
## Iteration: 87 bestvalit: 4.301173 bestmemit:  431.735845    0.112853   20.292797    1.503638    9.843571   -0.023273    0.055355
## Iteration: 88 bestvalit: 4.301173 bestmemit:  431.735845    0.112853   20.292797    1.503638    9.843571   -0.023273    0.055355
## Iteration: 89 bestvalit: 4.301173 bestmemit:  431.735845    0.112853   20.292797    1.503638    9.843571   -0.023273    0.055355
## Iteration: 90 bestvalit: 3.072398 bestmemit:  431.735845    0.112853   20.292797    1.503638    9.843571   -0.023273    0.027296
## Iteration: 91 bestvalit: 3.072398 bestmemit:  431.735845    0.112853   20.292797    1.503638    9.843571   -0.023273    0.027296
## Iteration: 92 bestvalit: 3.072398 bestmemit:  431.735845    0.112853   20.292797    1.503638    9.843571   -0.023273    0.027296
## Iteration: 93 bestvalit: 3.069272 bestmemit:  431.735845    0.117142   20.292797    1.503638    9.843571   -0.023273    0.027296
## Iteration: 94 bestvalit: 3.069272 bestmemit:  431.735845    0.117142   20.292797    1.503638    9.843571   -0.023273    0.027296
## Iteration: 95 bestvalit: 3.069272 bestmemit:  431.735845    0.117142   20.292797    1.503638    9.843571   -0.023273    0.027296
## Iteration: 96 bestvalit: 2.984702 bestmemit:  389.123730    0.102265   28.841937    1.870751    9.810743   -0.038394    0.011953
## Iteration: 97 bestvalit: 2.984702 bestmemit:  389.123730    0.102265   28.841937    1.870751    9.810743   -0.038394    0.011953
## Iteration: 98 bestvalit: 2.984702 bestmemit:  389.123730    0.102265   28.841937    1.870751    9.810743   -0.038394    0.011953
## Iteration: 99 bestvalit: 2.984702 bestmemit:  389.123730    0.102265   28.841937    1.870751    9.810743   -0.038394    0.011953
## Iteration: 100 bestvalit: 2.984702 bestmemit:  389.123730    0.102265   28.841937    1.870751    9.810743   -0.038394    0.011953
## Iteration: 101 bestvalit: 2.984702 bestmemit:  389.123730    0.102265   28.841937    1.870751    9.810743   -0.038394    0.011953
## Iteration: 102 bestvalit: 2.786511 bestmemit:  430.424118    0.103742   14.613617    0.759550    9.698384    0.043712   -0.032776
## Iteration: 103 bestvalit: 2.786511 bestmemit:  430.424118    0.103742   14.613617    0.759550    9.698384    0.043712   -0.032776
## Iteration: 104 bestvalit: 2.786511 bestmemit:  430.424118    0.103742   14.613617    0.759550    9.698384    0.043712   -0.032776
## Iteration: 105 bestvalit: 2.786511 bestmemit:  430.424118    0.103742   14.613617    0.759550    9.698384    0.043712   -0.032776
## Iteration: 106 bestvalit: 2.786511 bestmemit:  430.424118    0.103742   14.613617    0.759550    9.698384    0.043712   -0.032776
## Iteration: 107 bestvalit: 2.786511 bestmemit:  430.424118    0.103742   14.613617    0.759550    9.698384    0.043712   -0.032776
## Iteration: 108 bestvalit: 2.449609 bestmemit:  405.335044    0.104002   30.652301    2.031517    9.889521   -0.062861    0.013673
## Iteration: 109 bestvalit: 2.449609 bestmemit:  405.335044    0.104002   30.652301    2.031517    9.889521   -0.062861    0.013673
## Iteration: 110 bestvalit: 2.449609 bestmemit:  405.335044    0.104002   30.652301    2.031517    9.889521   -0.062861    0.013673
## Iteration: 111 bestvalit: 2.416582 bestmemit:  624.144745    0.110539   17.348768    1.165956    9.926090   -0.074172   -0.006543
## Iteration: 112 bestvalit: 2.416582 bestmemit:  624.144745    0.110539   17.348768    1.165956    9.926090   -0.074172   -0.006543
## Iteration: 113 bestvalit: 2.416582 bestmemit:  624.144745    0.110539   17.348768    1.165956    9.926090   -0.074172   -0.006543
## Iteration: 114 bestvalit: 2.416582 bestmemit:  624.144745    0.110539   17.348768    1.165956    9.926090   -0.074172   -0.006543
## Iteration: 115 bestvalit: 1.975567 bestmemit:  561.807558    0.110729    9.917919    4.501285    9.806397   -0.009725    0.048482
## Iteration: 116 bestvalit: 1.975567 bestmemit:  561.807558    0.110729    9.917919    4.501285    9.806397   -0.009725    0.048482
## Iteration: 117 bestvalit: 1.975567 bestmemit:  561.807558    0.110729    9.917919    4.501285    9.806397   -0.009725    0.048482
## Iteration: 118 bestvalit: 1.975567 bestmemit:  561.807558    0.110729    9.917919    4.501285    9.806397   -0.009725    0.048482
## Iteration: 119 bestvalit: 1.975567 bestmemit:  561.807558    0.110729    9.917919    4.501285    9.806397   -0.009725    0.048482
## Iteration: 120 bestvalit: 1.975567 bestmemit:  561.807558    0.110729    9.917919    4.501285    9.806397   -0.009725    0.048482
## Iteration: 121 bestvalit: 1.975567 bestmemit:  561.807558    0.110729    9.917919    4.501285    9.806397   -0.009725    0.048482
## Iteration: 122 bestvalit: 1.975567 bestmemit:  561.807558    0.110729    9.917919    4.501285    9.806397   -0.009725    0.048482
## Iteration: 123 bestvalit: 1.975567 bestmemit:  561.807558    0.110729    9.917919    4.501285    9.806397   -0.009725    0.048482
## Iteration: 124 bestvalit: 1.975567 bestmemit:  561.807558    0.110729    9.917919    4.501285    9.806397   -0.009725    0.048482
## Iteration: 125 bestvalit: 1.724043 bestmemit:  566.134988    0.114057    9.486160    3.679243    9.880730   -0.043408   -0.031316
## Iteration: 126 bestvalit: 1.724043 bestmemit:  566.134988    0.114057    9.486160    3.679243    9.880730   -0.043408   -0.031316
## Iteration: 127 bestvalit: 1.724043 bestmemit:  566.134988    0.114057    9.486160    3.679243    9.880730   -0.043408   -0.031316
## Iteration: 128 bestvalit: 1.724043 bestmemit:  566.134988    0.114057    9.486160    3.679243    9.880730   -0.043408   -0.031316
## Iteration: 129 bestvalit: 1.712154 bestmemit:  566.134988    0.116346    9.486160    3.679243    9.880730   -0.043408   -0.031316
## Iteration: 130 bestvalit: 1.712154 bestmemit:  566.134988    0.116346    9.486160    3.679243    9.880730   -0.043408   -0.031316
## Iteration: 131 bestvalit: 1.712154 bestmemit:  566.134988    0.116346    9.486160    3.679243    9.880730   -0.043408   -0.031316
## Iteration: 132 bestvalit: 1.712154 bestmemit:  566.134988    0.116346    9.486160    3.679243    9.880730   -0.043408   -0.031316
## Iteration: 133 bestvalit: 1.712154 bestmemit:  566.134988    0.116346    9.486160    3.679243    9.880730   -0.043408   -0.031316
## Iteration: 134 bestvalit: 1.712154 bestmemit:  566.134988    0.116346    9.486160    3.679243    9.880730   -0.043408   -0.031316
## Iteration: 135 bestvalit: 1.299255 bestmemit:  734.354653    0.115838    6.727759    2.859127    9.842684   -0.036713    0.048866
## Iteration: 136 bestvalit: 1.299255 bestmemit:  734.354653    0.115838    6.727759    2.859127    9.842684   -0.036713    0.048866
## Iteration: 137 bestvalit: 1.299255 bestmemit:  734.354653    0.115838    6.727759    2.859127    9.842684   -0.036713    0.048866
## Iteration: 138 bestvalit: 1.299255 bestmemit:  734.354653    0.115838    6.727759    2.859127    9.842684   -0.036713    0.048866
## Iteration: 139 bestvalit: 1.299255 bestmemit:  734.354653    0.115838    6.727759    2.859127    9.842684   -0.036713    0.048866
## Iteration: 140 bestvalit: 1.299255 bestmemit:  734.354653    0.115838    6.727759    2.859127    9.842684   -0.036713    0.048866
## Iteration: 141 bestvalit: 1.232035 bestmemit:  464.938535    0.105270    6.670577    4.162642    9.899531   -0.058988   -0.048299
## Iteration: 142 bestvalit: 1.232035 bestmemit:  464.938535    0.105270    6.670577    4.162642    9.899531   -0.058988   -0.048299
## Iteration: 143 bestvalit: 1.232035 bestmemit:  464.938535    0.105270    6.670577    4.162642    9.899531   -0.058988   -0.048299
## Iteration: 144 bestvalit: 1.232035 bestmemit:  464.938535    0.105270    6.670577    4.162642    9.899531   -0.058988   -0.048299
## Iteration: 145 bestvalit: 1.232035 bestmemit:  464.938535    0.105270    6.670577    4.162642    9.899531   -0.058988   -0.048299
## Iteration: 146 bestvalit: 1.232035 bestmemit:  464.938535    0.105270    6.670577    4.162642    9.899531   -0.058988   -0.048299
## Iteration: 147 bestvalit: 1.232035 bestmemit:  464.938535    0.105270    6.670577    4.162642    9.899531   -0.058988   -0.048299
## Iteration: 148 bestvalit: 1.232035 bestmemit:  464.938535    0.105270    6.670577    4.162642    9.899531   -0.058988   -0.048299
## Iteration: 149 bestvalit: 1.232035 bestmemit:  464.938535    0.105270    6.670577    4.162642    9.899531   -0.058988   -0.048299
## Iteration: 150 bestvalit: 1.232035 bestmemit:  464.938535    0.105270    6.670577    4.162642    9.899531   -0.058988   -0.048299
## Iteration: 151 bestvalit: 1.232035 bestmemit:  464.938535    0.105270    6.670577    4.162642    9.899531   -0.058988   -0.048299
## Iteration: 152 bestvalit: 1.232035 bestmemit:  464.938535    0.105270    6.670577    4.162642    9.899531   -0.058988   -0.048299
## Iteration: 153 bestvalit: 1.232035 bestmemit:  464.938535    0.105270    6.670577    4.162642    9.899531   -0.058988   -0.048299
## Iteration: 154 bestvalit: 1.232035 bestmemit:  464.938535    0.105270    6.670577    4.162642    9.899531   -0.058988   -0.048299
## Iteration: 155 bestvalit: 1.232035 bestmemit:  464.938535    0.105270    6.670577    4.162642    9.899531   -0.058988   -0.048299
## Iteration: 156 bestvalit: 1.232035 bestmemit:  464.938535    0.105270    6.670577    4.162642    9.899531   -0.058988   -0.048299
## Iteration: 157 bestvalit: 1.232035 bestmemit:  464.938535    0.105270    6.670577    4.162642    9.899531   -0.058988   -0.048299
## Iteration: 158 bestvalit: 1.232035 bestmemit:  464.938535    0.105270    6.670577    4.162642    9.899531   -0.058988   -0.048299
## Iteration: 159 bestvalit: 1.232035 bestmemit:  464.938535    0.105270    6.670577    4.162642    9.899531   -0.058988   -0.048299
## Iteration: 160 bestvalit: 1.232035 bestmemit:  464.938535    0.105270    6.670577    4.162642    9.899531   -0.058988   -0.048299
## Iteration: 161 bestvalit: 1.232035 bestmemit:  464.938535    0.105270    6.670577    4.162642    9.899531   -0.058988   -0.048299
## Iteration: 162 bestvalit: 1.232035 bestmemit:  464.938535    0.105270    6.670577    4.162642    9.899531   -0.058988   -0.048299
## Iteration: 163 bestvalit: 1.232035 bestmemit:  464.938535    0.105270    6.670577    4.162642    9.899531   -0.058988   -0.048299
## Iteration: 164 bestvalit: 1.232035 bestmemit:  464.938535    0.105270    6.670577    4.162642    9.899531   -0.058988   -0.048299
## Iteration: 165 bestvalit: 1.232035 bestmemit:  464.938535    0.105270    6.670577    4.162642    9.899531   -0.058988   -0.048299
## Iteration: 166 bestvalit: 1.232035 bestmemit:  464.938535    0.105270    6.670577    4.162642    9.899531   -0.058988   -0.048299
## Iteration: 167 bestvalit: 1.232035 bestmemit:  464.938535    0.105270    6.670577    4.162642    9.899531   -0.058988   -0.048299
## Iteration: 168 bestvalit: 1.232035 bestmemit:  464.938535    0.105270    6.670577    4.162642    9.899531   -0.058988   -0.048299
## Iteration: 169 bestvalit: 1.232035 bestmemit:  464.938535    0.105270    6.670577    4.162642    9.899531   -0.058988   -0.048299
## Iteration: 170 bestvalit: 1.232035 bestmemit:  464.938535    0.105270    6.670577    4.162642    9.899531   -0.058988   -0.048299
## Iteration: 171 bestvalit: 1.232035 bestmemit:  464.938535    0.105270    6.670577    4.162642    9.899531   -0.058988   -0.048299
## Iteration: 172 bestvalit: 1.232035 bestmemit:  464.938535    0.105270    6.670577    4.162642    9.899531   -0.058988   -0.048299
## Iteration: 173 bestvalit: 1.232035 bestmemit:  464.938535    0.105270    6.670577    4.162642    9.899531   -0.058988   -0.048299
## Iteration: 174 bestvalit: 1.232035 bestmemit:  464.938535    0.105270    6.670577    4.162642    9.899531   -0.058988   -0.048299
## Iteration: 175 bestvalit: 1.232035 bestmemit:  464.938535    0.105270    6.670577    4.162642    9.899531   -0.058988   -0.048299
## Iteration: 176 bestvalit: 1.232035 bestmemit:  464.938535    0.105270    6.670577    4.162642    9.899531   -0.058988   -0.048299
## Iteration: 177 bestvalit: 1.232035 bestmemit:  464.938535    0.105270    6.670577    4.162642    9.899531   -0.058988   -0.048299
## Iteration: 178 bestvalit: 1.232035 bestmemit:  464.938535    0.105270    6.670577    4.162642    9.899531   -0.058988   -0.048299
## Iteration: 179 bestvalit: 1.232035 bestmemit:  464.938535    0.105270    6.670577    4.162642    9.899531   -0.058988   -0.048299
## Iteration: 180 bestvalit: 1.232035 bestmemit:  464.938535    0.105270    6.670577    4.162642    9.899531   -0.058988   -0.048299
## Iteration: 181 bestvalit: 1.232035 bestmemit:  464.938535    0.105270    6.670577    4.162642    9.899531   -0.058988   -0.048299
## Iteration: 182 bestvalit: 1.232035 bestmemit:  464.938535    0.105270    6.670577    4.162642    9.899531   -0.058988   -0.048299
## Iteration: 183 bestvalit: 1.232035 bestmemit:  464.938535    0.105270    6.670577    4.162642    9.899531   -0.058988   -0.048299
## Iteration: 184 bestvalit: 1.232035 bestmemit:  464.938535    0.105270    6.670577    4.162642    9.899531   -0.058988   -0.048299
## Iteration: 185 bestvalit: 1.232035 bestmemit:  464.938535    0.105270    6.670577    4.162642    9.899531   -0.058988   -0.048299
## Iteration: 186 bestvalit: 1.232035 bestmemit:  464.938535    0.105270    6.670577    4.162642    9.899531   -0.058988   -0.048299
## Iteration: 187 bestvalit: 1.232035 bestmemit:  464.938535    0.105270    6.670577    4.162642    9.899531   -0.058988   -0.048299
## Iteration: 188 bestvalit: 1.232035 bestmemit:  464.938535    0.105270    6.670577    4.162642    9.899531   -0.058988   -0.048299
## Iteration: 189 bestvalit: 1.232035 bestmemit:  464.938535    0.105270    6.670577    4.162642    9.899531   -0.058988   -0.048299
## Iteration: 190 bestvalit: 1.232035 bestmemit:  464.938535    0.105270    6.670577    4.162642    9.899531   -0.058988   -0.048299
## Iteration: 191 bestvalit: 1.232035 bestmemit:  464.938535    0.105270    6.670577    4.162642    9.899531   -0.058988   -0.048299
## Iteration: 192 bestvalit: 1.232035 bestmemit:  464.938535    0.105270    6.670577    4.162642    9.899531   -0.058988   -0.048299
## Iteration: 193 bestvalit: 1.232035 bestmemit:  464.938535    0.105270    6.670577    4.162642    9.899531   -0.058988   -0.048299
## Iteration: 194 bestvalit: 1.232035 bestmemit:  464.938535    0.105270    6.670577    4.162642    9.899531   -0.058988   -0.048299
## Iteration: 195 bestvalit: 1.232035 bestmemit:  464.938535    0.105270    6.670577    4.162642    9.899531   -0.058988   -0.048299
## Iteration: 196 bestvalit: 1.232035 bestmemit:  464.938535    0.105270    6.670577    4.162642    9.899531   -0.058988   -0.048299
## Iteration: 197 bestvalit: 1.232035 bestmemit:  464.938535    0.105270    6.670577    4.162642    9.899531   -0.058988   -0.048299
## Iteration: 198 bestvalit: 1.232035 bestmemit:  464.938535    0.105270    6.670577    4.162642    9.899531   -0.058988   -0.048299
## Iteration: 199 bestvalit: 1.232035 bestmemit:  464.938535    0.105270    6.670577    4.162642    9.899531   -0.058988   -0.048299
## Iteration: 200 bestvalit: 1.232035 bestmemit:  464.938535    0.105270    6.670577    4.162642    9.899531   -0.058988   -0.048299

best_params <- result$optim$bestmem
names(best_params) <- c("tc", "beta", "omega", "phi", "A", "B", "C")

# 计算拟合值
fitted_values <- lppl(t, best_params["tc"], best_params["beta"],
                      best_params["omega"], best_params["phi"],
                      best_params["A"], best_params["B"], best_params["C"])
predicted_prices <- exp(fitted_values)

# 预测未来120天（修正行数不一致问题）
future_t <- seq(max(t), max(t) + 119)  # 改为119确保总天数120
future_fitted <- sapply(future_t, function(x) {
  if (x >= best_params["tc"] - 1e-5) {
    best_params["A"]
  } else {
    lppl(x, best_params["tc"], best_params["beta"],
         best_params["omega"], best_params["phi"],
         best_params["A"], best_params["B"], best_params["C"])
  }
})
future_prices <- exp(future_fitted)
future_dates <- seq(max(dates), by = "day", length.out = 120)

# 可视化结果（确保数据长度一致）
plot_data <- data.frame(
  Date = c(dates, future_dates),
  Price = c(prices, future_prices),
  Type = c(rep("Actual", length(prices)), rep("Predicted", length(future_prices)))
)

p1 <- ggplot(plot_data, aes(x = Date, y = Price, color = Type)) +
  geom_line() +
  geom_vline(xintercept = as.Date(dates[1]) + best_params["tc"], linetype = "dashed") +
  labs(title = "纳斯达克指数LPPL模型拟合与预测",
       y = "指数值",
       x = "日期") +
  scale_color_manual(values = c("Actual" = "blue", "Predicted" = "red")) +
  theme_minimal()

# 分析对数周期振荡
oscillations <- best_params["C"] * (best_params["tc"] - t)^best_params["beta"] * 
  cos(best_params["omega"] * log(best_params["tc"] - t) + best_params["phi"])

# 可视化振荡部分
osc_data <- data.frame(
  Date = dates,
  Oscillation = oscillations
)

p2 <- ggplot(osc_data, aes(x = Date, y = Oscillation)) +
  geom_line(color = "blue") +
  geom_hline(yintercept = 0, linetype = "dashed", color = "gray") +
  labs(title = "LPPL模型中的对数周期振荡",
       y = "振荡幅度",
       x = "日期") +
  theme_minimal()

# 预测未来价格走势（增加稳定性检查）
future_t <- seq(max(t), max(t) + 120, by = 1)  # 预测未来120天
future_fitted <- numeric(length(future_t))

for(i in seq_along(future_t)) {
  if(future_t[i] >= best_params["tc"] - 1) {
    future_fitted[i] <- fitted_values[length(fitted_values)]
  } else {
    future_fitted[i] <- lppl(future_t[i], best_params["tc"], best_params["beta"], 
                             best_params["omega"], best_params["phi"], 
                             best_params["A"], best_params["B"], best_params["C"])
  }
}

future_prices <- exp(future_fitted)
future_prices <- ifelse(is.finite(future_prices), future_prices, NA)

future_dates <- seq(max(dates), by = "day", length.out = length(future_t))

# 合并历史与预测数据
prediction_data <- data.frame(
  Date = c(as.Date(dates), future_dates),
  Price = c(prices, future_prices),
  Type = c(rep("历史", length(prices)), rep("预测", length(future_prices)))
)

# 可视化预测结果
p3 <- ggplot(prediction_data, aes(x = Date, y = Price, color = Type)) +
  geom_line() +
  geom_vline(xintercept = as.numeric(max(dates)), linetype = "dashed", color = "gray") +
  labs(title = "纳斯达克指数LPPL模型预测",
       y = "指数值",
       x = "日期") +
  scale_color_manual(values = c("历史" = "black", "预测" = "red")) +
  theme_minimal()

print(p1)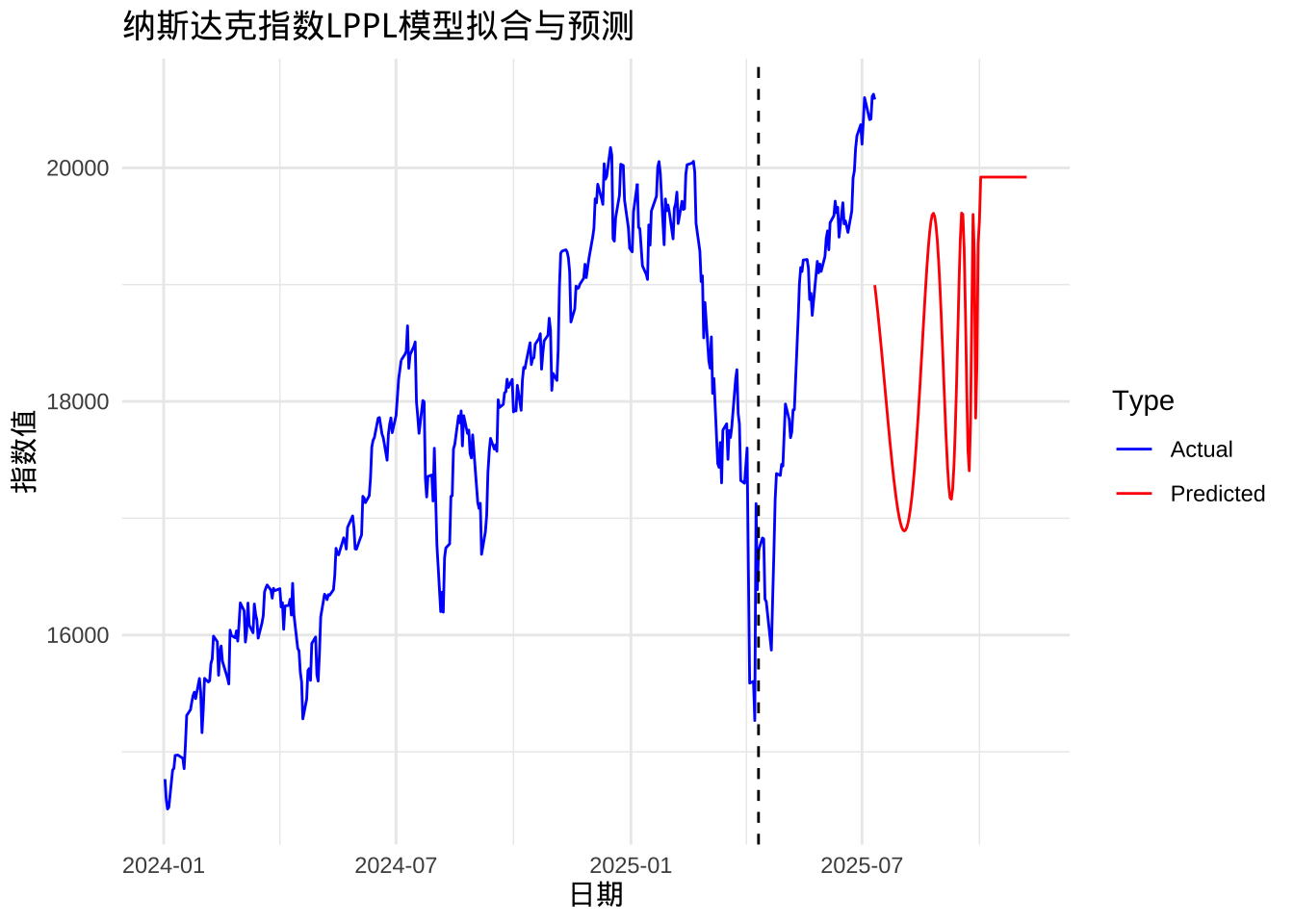

print(p2)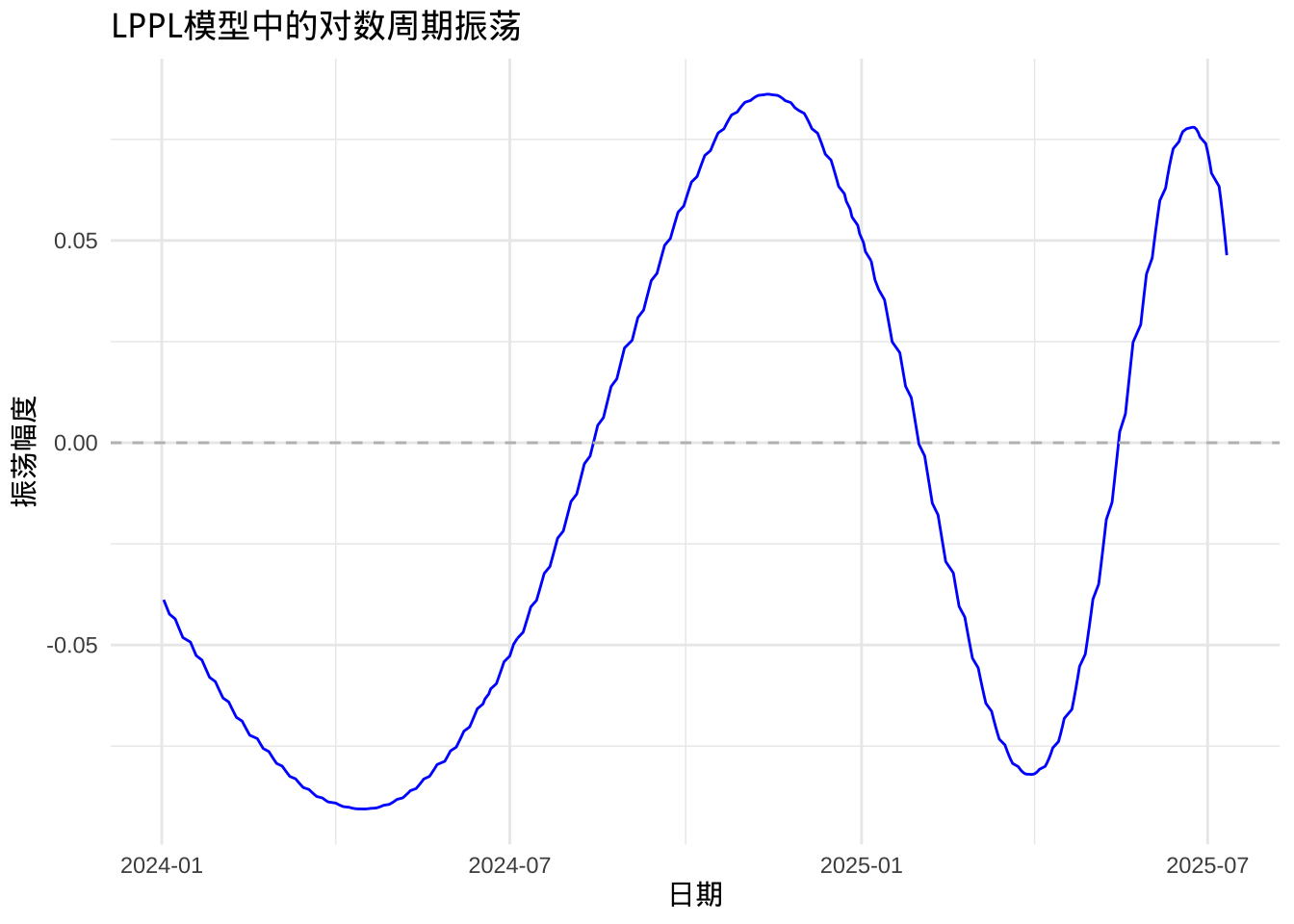

print(p3)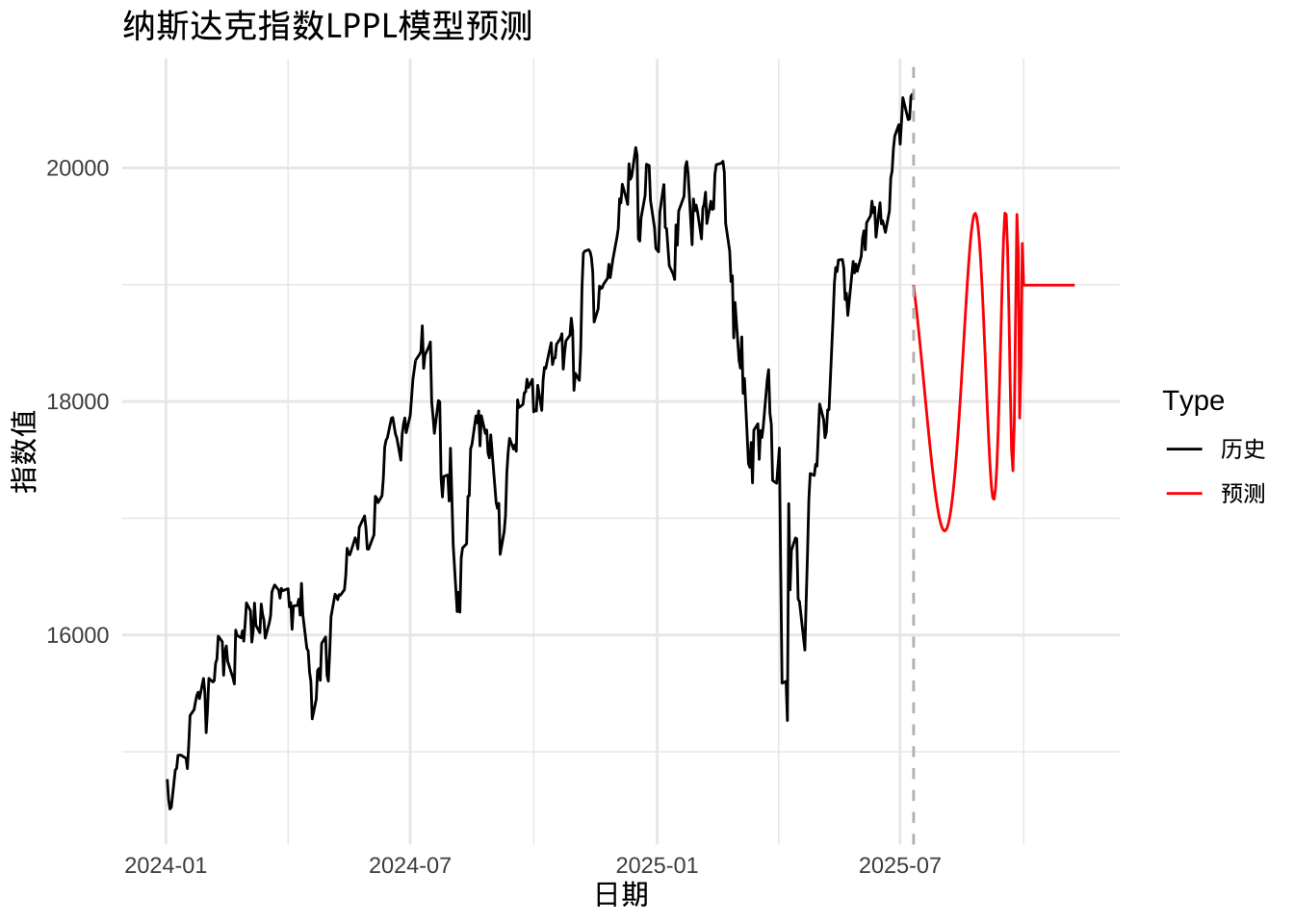

# 输出关键参数
cat("LPPL模型参数估计结果:\n")

## LPPL模型参数估计结果:

print(best_params)

##           tc         beta        omega          phi            A            B 
## 464.93853499   0.10526956   6.67057660   4.16264248   9.89953086  -0.05898808 
##            C 
##  -0.04829888

cat("\n预测的临界时间点:", as.character(as.Date(dates[1] + round(best_params["tc"]))), "\n")

## 
## 预测的临界时间点: 2025-04-11

实证分析结果

通过对纳斯达克指数的 LPPL模型拟合，我们得到以下主要发现：

泡沫特征识别：模型成功捕捉到了纳斯达克指数在特定时期的加速上涨特征，以及伴随的对数周期性振荡，这与理论上的泡沫形成过程高度一致。临界时间预测：基于参数估计结果，模型预测了潜在的临界时间点 \(t_c\)，这一时间点可视为泡沫可能破裂的理论时间。实际应用中，可结合其他指标（如交易量、波动率）进行综合判断。

振荡周期分析：对数周期振荡的频率参数 \(\omega\) 反映了市场情绪的波动周期。通过分析振荡部分，我们可以识别市场参与者的从众行为强度及其变化趋势。

预测局限性：尽管 LPPL 模型在识别泡沫特征方面表现出色，但预测的临界时间点存在一定误差，特别是在市场环境发生重大变化时。因此，该模型更适合作为预警工具而非精确预测工具。

模型改进与应用

建议为提高 LPPL 模型的实用性，可考虑以下改进方向：多窗口分析：采用滚动窗口方法，定期重新估计模型参数，以适应市场结构的变化。集成其他指标：结合技术指标（如 RSI、MACD）和基本面因素，构建更全面的市场预警系统。参数优化改进：探索更高效的参数优化算法，提高模型拟合的稳定性和准确性。风险管理应用：将 LPPL 模型纳入风险管理框架，当检测到显著泡沫特征时，调整仓位或实施对冲策略。

结论

LPPL 模型为分析金融市场中的泡沫现象提供了有力工具。通过对纳斯达克指数的实证分析，我们验证了模型在识别价格加速上涨和对数周期振荡方面的有效性。尽管模型预测存在一定局限性，但作为一种早期预警机制，它能够帮助投资者识别潜在的市场风险，及时调整投资策略。未来研究可进一步探索 LPPL 模型与其他市场分析方法的结合，以提高预测准确性和实用性。

基于 LPPL 模型的纳斯达克指数泡沫检测与预测分析

摘要

LPPL 模型理论基础

R 语言实现 LPPL 模型分析

实证分析结果

模型改进与应用

结论